题目内容
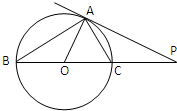 (2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为
(2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为4π
4π
.分析:由已知中,已知PA是圆O的切线,切点为A,直线PO交圆O于B,C两点,AC=2,∠PAB=120°,我们根据切线的性质,等腰三角形两底角相等,直径所对圆周角为直角,30°所对的直角边等于斜边的一半,求出圆的半径,代入圆面积公式,即可得到答案.
解答:解:∵PA是圆O的切线,
∴OA⊥AP
又∵∠PAB=120°
∴∠BAO=∠ABO=30°
又∵在Rt△ABC中,AC=2
∴BC=4,即圆O的直径2R=4
∴圆O的面积S=πR2=4π
故答案为:4π.
∴OA⊥AP
又∵∠PAB=120°
∴∠BAO=∠ABO=30°
又∵在Rt△ABC中,AC=2
∴BC=4,即圆O的直径2R=4
∴圆O的面积S=πR2=4π
故答案为:4π.
点评:本题考查的知识点是切线的性质,圆周角定理,其中根据已知条件,求出圆的半径是解答本题的关键.

练习册系列答案
相关题目
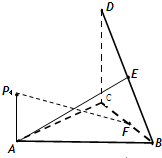 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.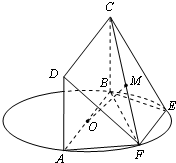 (2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.