题目内容
如图所示是一个由边长为1个单位的12个正方形组成的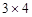 棋盘,规定每次只能沿正方形的边运动,且只能走一个单位,则从
棋盘,规定每次只能沿正方形的边运动,且只能走一个单位,则从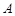 走到
走到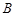 的最短路径的走法有 种
的最短路径的走法有 种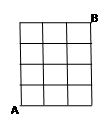
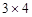 棋盘,规定每次只能沿正方形的边运动,且只能走一个单位,则从
棋盘,规定每次只能沿正方形的边运动,且只能走一个单位,则从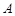 走到
走到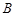 的最短路径的走法有 种
的最短路径的走法有 种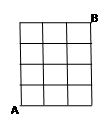
35
要想从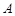 走到
走到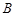 的路径最短,只需走7个单位,并且这7个单位中,有3个横单位和4个竖单位;在这7各单位中,只要3个横单位确定,走法就确定;所以
的路径最短,只需走7个单位,并且这7个单位中,有3个横单位和4个竖单位;在这7各单位中,只要3个横单位确定,走法就确定;所以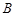 的最短路径的走法有
的最短路径的走法有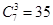 种
种
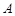 走到
走到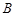 的路径最短,只需走7个单位,并且这7个单位中,有3个横单位和4个竖单位;在这7各单位中,只要3个横单位确定,走法就确定;所以
的路径最短,只需走7个单位,并且这7个单位中,有3个横单位和4个竖单位;在这7各单位中,只要3个横单位确定,走法就确定;所以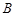 的最短路径的走法有
的最短路径的走法有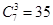 种
种
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
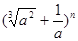 的展开式含
的展开式含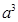 项,则最小的自然数
项,则最小的自然数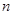 是( ▲ )
是( ▲ )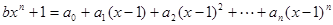 对任意
对任意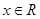 恒成立,且
恒成立,且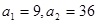 ,则
,则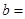 ( )
( )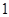
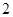
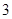
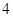
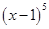 的展开式中,
的展开式中,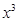 的系数为( ▲ )
的系数为( ▲ )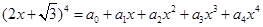 ,则
,则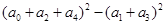 的值为( )
的值为( )
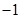
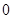
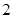
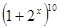 的展开式中的第
的展开式中的第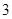 项为
项为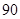 ,则
,则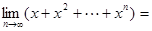 ___________.
___________.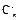 +2
+2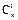 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为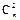 +22
+22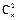 =
=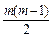 +2n(n-1)=
+2n(n-1)=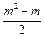 +(11-m)(
+(11-m)(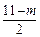 -1)=(m-
-1)=(m-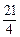 )2+
)2+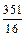 .
. 33,
33,