题目内容
已知函数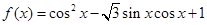 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若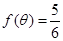 ,
,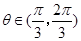 ,求
,求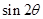 的值.
的值.
(1)函数 的增区间为
的增区间为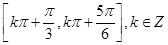 ;(2)
;(2)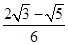 .
.
解析试题分析:(1)先由正余弦的二倍角公式及和差公式化简函数得到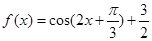 ,进而将
,进而将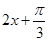 当成整体,由余弦的单调增区间得到
当成整体,由余弦的单调增区间得到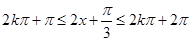 ,从中求解即可得出函数
,从中求解即可得出函数 的单调增区间;(2)先由
的单调增区间;(2)先由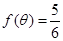 得到
得到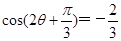 ,由
,由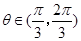 ,得出
,得出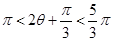 ,进而应用同角三角函数的基本关系式得到
,进而应用同角三角函数的基本关系式得到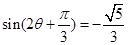 ,再将
,再将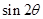 变形为
变形为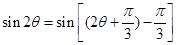 ,应用两角差的正弦公式展开计算即可.
,应用两角差的正弦公式展开计算即可.
试题解析:(1)因为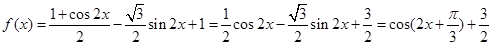
由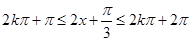
解得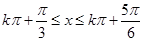
所以函数 的增区间为
的增区间为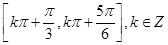
(2)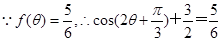
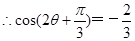 ,又
,又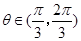 ,所以
,所以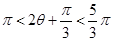
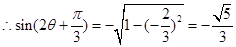
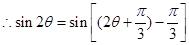
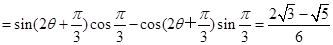 .
.
考点:1.倍角公式;2.三角函数的图像与性质;3.同角三角函数的基本关系式;4.两角和差公式.

练习册系列答案
相关题目
 ,其中x∈R,θ为参数,且0≤θ≤2π.
,其中x∈R,θ为参数,且0≤θ≤2π. 时,判断函数f(x)是否有极值;
时,判断函数f(x)是否有极值;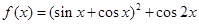 .
.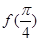 值;
值;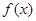 的最小值正周期;
的最小值正周期; 中,已知
中,已知 ,向量
,向量 ,
, ,且
,且 .
. 的值;
的值; 在边
在边 上,且
上,且 ,
, ,求△
,求△
 的最小正周期;
的最小正周期;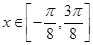 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。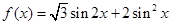 .
.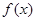 的最小正周期;
的最小正周期; 上的最大值和最小值.
上的最大值和最小值. =
=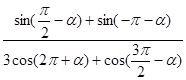 ; (2)若
; (2)若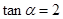 ,求
,求 ,设函数
,设函数 .
. ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积.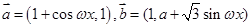 (
(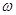 为常数且
为常数且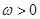 ),函数
),函数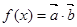 在
在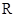 上的最大值为
上的最大值为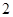 .
. 的值;
的值;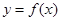 的图象向右平移
的图象向右平移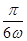 个单位,可得函数
个单位,可得函数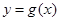 的图象,若
的图象,若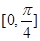 上为增函数,求
上为增函数,求