题目内容
已知函数f(x)=4x3-3x2cosθ+ ,其中x∈R,θ为参数,且0≤θ≤2π.
,其中x∈R,θ为参数,且0≤θ≤2π.
(1)当 时,判断函数f(x)是否有极值;
时,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(3)若对(2)中所求的取值范围内的任意参数θ,函数f(x)在区间(2A-1,A)内都是增函数,求实数A的取值范围.
(1) 无极值;(2) θ的取值范围为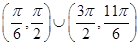 ;(3) A的取值范围是
;(3) A的取值范围是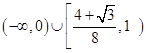 .
.
解析试题分析:(1)由题得f(x)=4x3 ,由幂函数性质知,在R上为增函数,无极值;(2)对原函数求导且令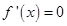 ,解得
,解得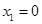 或
或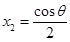 ,当
,当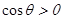 时,可求得极小值
时,可求得极小值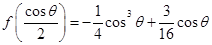 ,令
,令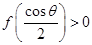 得
得 ,当
,当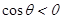 ,所求极小值不会小于零,可得
,所求极小值不会小于零,可得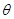 范围;(3) 函数f(x)在区间(2A-1,A)内都是增函数,则A需满足不等式组
范围;(3) 函数f(x)在区间(2A-1,A)内都是增函数,则A需满足不等式组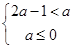 或
或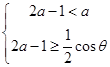 ,解得
,解得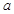 的范围.
的范围.
解:(1)当 时,f(x)=4x3,则f(x)在(-∞,+∞)内是增函数,故无极值. 2分
时,f(x)=4x3,则f(x)在(-∞,+∞)内是增函数,故无极值. 2分
(2)f′(x)=12x2-6xcosθ,
令f′(x)=0,得x1=0,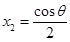 . 3分
. 3分
当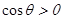 时,容易判断f(x)在(-∞,0],
时,容易判断f(x)在(-∞,0], 上是增函数,在
上是增函数,在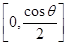 上是减函数,
上是减函数,
故f(x)在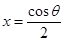 处取得极小值
处取得极小值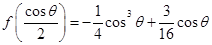 5分
5分
由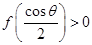 ,即
,即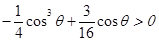 ,可得
,可得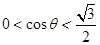 .
.
由于0≤θ≤2π,故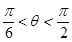 或
或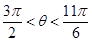 . 7分
. 7分
同理,可知当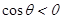 时,f(x)在x=0处取得极小值
时,f(x)在x=0处取得极小值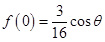 ,此时,当f(0)>0时,
,此时,当f(0)>0时,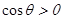 ,与
,与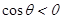 相矛盾,所以当
相矛盾,所以当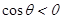 时,f(x)的极小值不会大于零.
时,f(x)的极小值不会大于零.
综上,要使函数f(x)在(-∞,+∞)的极小值大于零,θ的取值范围为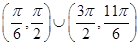 . 9分
. 9分
(3)由(2),知函数f(x)在区间(-∞,0]与 内都是增函数,由题设:函数在(2A-1,A)内是增函数,则A需满足不等式组
内都是增函数,由题设:函数在(2A-1,A)内是增函数,则A需满足不等式组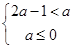 或
或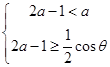 (其中θ∈
(其中θ∈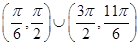 时,
时,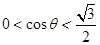 ). 12分
). 12分
从而可以解得A≤0或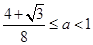 ,
,
即A的取值范围是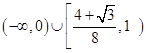 . 14分
. 14分
考点:函数的极值,由三角函数求角的范围,函数的单调性.

练习册系列答案
相关题目
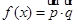 ,而
,而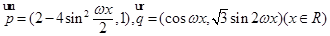 .
.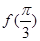 最大,求
最大,求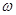 能取到的最小正数值.
能取到的最小正数值.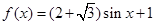 且
且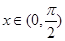 ,求
,求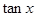 .
.
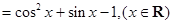 .
.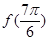 的值;
的值;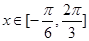 时,求
时,求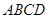 内修建一个三角形隔离区以投放净化物质,其形状为三角形
内修建一个三角形隔离区以投放净化物质,其形状为三角形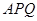 ,其中
,其中 位于边
位于边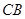 上,
上,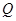 位于边
位于边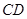 上.已知
上.已知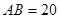 米,
米,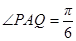 ,设
,设 ,记
,记 ,当
,当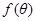 越大,则污水净化效果越好.
越大,则污水净化效果越好.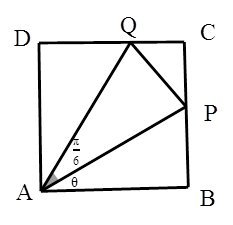
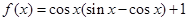 .
. 的最小正周期;
的最小正周期;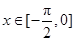 时,求函数
时,求函数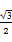 sinωx-sin2
sinωx-sin2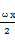 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围. 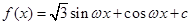 (
( ,
,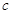 是实数常数)的图像上的一个最高点
是实数常数)的图像上的一个最高点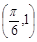 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是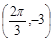 ,
,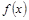 的解析式及其单调增区间;
的解析式及其单调增区间;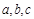 ,且
,且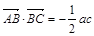 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当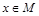 时,试求函数
时,试求函数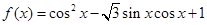 .
. 的单调递增区间;
的单调递增区间;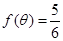 ,
,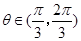 ,求
,求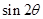 的值.
的值.