题目内容
(2013•汕头二模)已知抛物线和双曲线都经过点M(1,2),它们在x轴上有共同焦点,对称轴是坐标轴,抛物线的顶点为坐标原点.
(1)求抛物线和双曲线标准方程;
(2)已知动直线m过点P(3,0),交抛物线于A,B两点,记以线段AP为直径的圆为圆C,求证:存在垂直于x轴的直线l被圆C截得的弦长为定值,并求出直线l的方程.
(1)求抛物线和双曲线标准方程;
(2)已知动直线m过点P(3,0),交抛物线于A,B两点,记以线段AP为直径的圆为圆C,求证:存在垂直于x轴的直线l被圆C截得的弦长为定值,并求出直线l的方程.
分析:(1)设抛物线的方程为 y2=2px(p>0),把点M(1,2)代入求得p的值,即可求得抛物线的方程.对于双曲线,由焦点坐标求得c的值,由双曲线的定义求得a,从而求得b的值,从而求得双曲线的标准方程.
(2)由题意可得,AP的中点为C,设A(x1,y1),则C(
,
).设D、E是圆C上的两个点,且DE垂直于x轴,DE的中点为H,点D(x2,y2),则H(x2,y3),求得|DC|和|CH|、|DH|2,可得当x2=2时,|DH|2=2,故弦长为|DE|=2|DH|=2
为定值,由此可得结论
(2)由题意可得,AP的中点为C,设A(x1,y1),则C(
| x1+3 |
| 2 |
| y1 |
| 2 |
| 2 |
解答:解:(1)设抛物线的方程为 y2=2px(p>0),把点M(1,2)代入求得p=2,
∴抛物线的方程为 y2=4x,焦点坐标为F1(1,0).
对于双曲线,一个焦点坐标为F1(1,0),则另一个焦点坐标为F2(-1,0),
故c=1,2a=||MF1|-|MF2||=2
-2,∴a=
-1,∴b2=c2-a2=2
-2.
故双曲线的标准方程为
-
=1.
(2)由题意可得,AP的中点为C,设A(x1,y1),则C(
,
).
设D、E是圆C上的两个点,且DE垂直于x轴,DE的中点为H,点D(x2,y2),则H(x2,y3),
|DC|=
|AP|=
,|CH|=|
-x2|=
|(x1-2x2)+3|,
|DH|2=|DC|2-|HC|2=
[(x1-3)2+y12]-
[x1-2x2)+3]2=(x2-2)x1-x22+3x2
由x2的任意性可得,当x2=2时,|DH|2=-4+6=2,故弦长为|DE|=2|DH|=2
为定值.
故存在垂直于x轴的直线l(即直线DE),倍圆截得的弦长为定值,直线l的方程为 x=2.
∴抛物线的方程为 y2=4x,焦点坐标为F1(1,0).
对于双曲线,一个焦点坐标为F1(1,0),则另一个焦点坐标为F2(-1,0),
故c=1,2a=||MF1|-|MF2||=2
| 2 |
| 2 |
| 2 |
故双曲线的标准方程为
| x2 | ||
3-2
|
| y2 | ||
2
|
(2)由题意可得,AP的中点为C,设A(x1,y1),则C(
| x1+3 |
| 2 |
| y1 |
| 2 |
设D、E是圆C上的两个点,且DE垂直于x轴,DE的中点为H,点D(x2,y2),则H(x2,y3),
|DC|=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1-3)2+y12 |
| x1+3 |
| 2 |
| 1 |
| 2 |
|DH|2=|DC|2-|HC|2=
| 1 |
| 4 |
| 1 |
| 4 |
由x2的任意性可得,当x2=2时,|DH|2=-4+6=2,故弦长为|DE|=2|DH|=2
| 2 |
故存在垂直于x轴的直线l(即直线DE),倍圆截得的弦长为定值,直线l的方程为 x=2.
点评:本题主要考查用待定系数法求抛物线和双曲线的标准方程,直线和圆相交的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为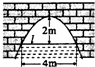 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽