Question

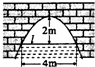（2013•汕头二模）如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米，水位下降2米后水面宽

4

2

米．

Answer 1

分析：先建立直角坐标系，将A点代入抛物线方程求得m，得到抛物线方程，再把y=-4代入抛物线方程求得x₀进而得到答案．

解答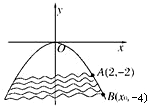：解：如图建立直角坐标系，设抛物线方程为x²=my，
将A（2，-2）代入x²=my，
得m=-2
∴x²=-2y，代入B（x₀，-4）得x₀=2

2

，
故水面宽为4

2

m．
故答案为：4

2

．

点评：本题主要考查抛物线的应用．考查了学生利用抛物线解决实际问题 的能力．