题目内容
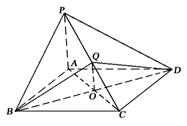
( 12分)如图,在四棱锥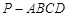 中,侧面
中,侧面 是正三角形,底面
是正三角形,底面 是边长为2的正方形,侧面
是边长为2的正方形,侧面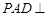 平面
平面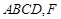 为
为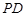 的中点.
的中点.
①求证: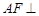 平面
平面 ;
;
②求直线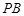 与平面
与平面 所成角的正切值.
所成角的正切值.
(Ⅰ)证明:见解析;(Ⅱ)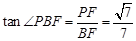 ,即求.
,即求.
解析试题分析:(Ⅰ)证明AF⊥平面PCD,利用线面垂直的判定定理,只需证明AF⊥PD,CD⊥AF即可;
(Ⅱ)证明∠PBF为直线PB与平面ABF所成的角,求出PF,BF的长,即可得出结论.
(Ⅰ)证明:如图,由 是正三角形,
是正三角形,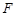 为
为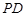 中点,所以
中点,所以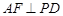 ,又因为平面
,又因为平面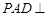 平面
平面 ,
,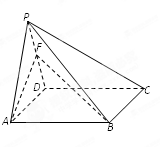
且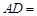 面
面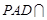 面
面 ;
;
又底面 为正方形,即
为正方形,即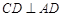
所以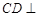 平面
平面 ,而
,而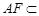 平面
平面 ,
,
所以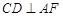 ,且
,且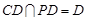 ,
,
所以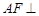 平面
平面 .………………6分;
.………………6分;
(Ⅱ)由(Ⅰ)证明可知,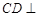 平面
平面 ,
,
所以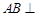 平面
平面
所以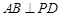 ,又由(Ⅰ)知
,又由(Ⅰ)知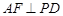 ,且
,且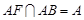 ,
,
所以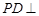 平面
平面 ,
,
即 为直线
为直线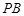 与平面
与平面 所成的角…………………9分
所成的角…………………9分
且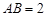 ,易知
,易知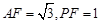 ,
,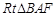 中,
中,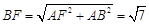 ,
,
所以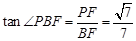 ,即求.………………12分
,即求.………………12分
考点:本题考查线面垂直,考查线面角,属于中档题.
点评:解题的关键是正确运用线面垂直的判定,作出线面角.

练习册系列答案
相关题目

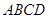 和矩形
和矩形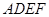 所在平面相互垂直,
所在平面相互垂直,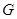 是
是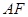 的中点.
的中点. 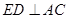 ;
;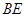 与平面
与平面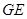 与
与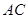 所成角的余弦值.
所成角的余弦值.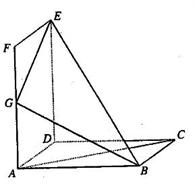
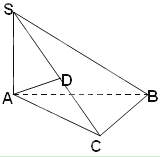
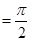 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE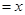 ,G是BC的中点.沿EF将梯形ABCD翻折,
,G是BC的中点.沿EF将梯形ABCD翻折,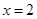 时,求证:BD⊥EG ;
时,求证:BD⊥EG ;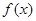 ,求
,求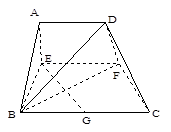
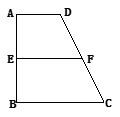
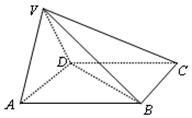
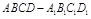 的底面
的底面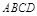 是菱形,
是菱形,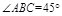 ,其侧面展开图是边长为
,其侧面展开图是边长为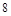 的正方形.
的正方形.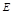 、
、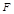 分别是侧棱
分别是侧棱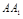 、
、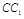 上的动点,
上的动点,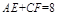 .
.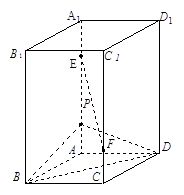
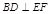 ;
;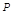 在棱
在棱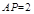 ,若
,若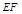 ∥平面
∥平面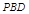 ,求
,求 .
.