题目内容
直四棱柱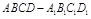 的底面
的底面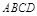 是菱形,
是菱形,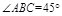 ,其侧面展开图是边长为
,其侧面展开图是边长为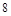 的正方形.
的正方形.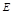 、
、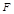 分别是侧棱
分别是侧棱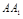 、
、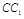 上的动点,
上的动点,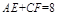 .
.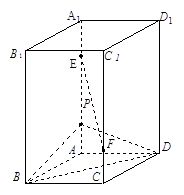
(Ⅰ)证明: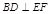 ;
;
(Ⅱ)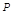 在棱
在棱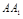 上,且
上,且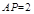 ,若
,若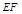 ∥平面
∥平面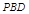 ,求
,求 .
.
(Ⅰ)见解析 (Ⅱ)2
解析

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
题目内容
直四棱柱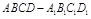 的底面
的底面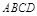 是菱形,
是菱形,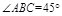 ,其侧面展开图是边长为
,其侧面展开图是边长为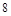 的正方形.
的正方形.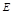 、
、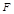 分别是侧棱
分别是侧棱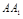 、
、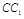 上的动点,
上的动点,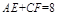 .
.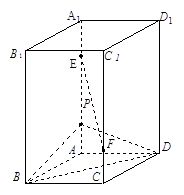
(Ⅰ)证明: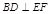 ;
;
(Ⅱ)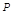 在棱
在棱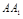 上,且
上,且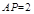 ,若
,若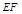 ∥平面
∥平面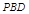 ,求
,求 .
.
(Ⅰ)见解析 (Ⅱ)2
解析

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案