题目内容
10.已知各项均为正数的数列{an}满足a1=2,an+12=2an2+anan+1,其中n∈N+,设数列{bn}满足bn=$\frac{{na}_{n}}{(2n+1){2}^{n}}$,若存在正整数m,n使得b1,bm,bn成等比数列,则m+n=14.分析 由已知条件推导出数列{an}是公比为2的等比数列.由此能求出an=2n,n∈N*.由bn=$\frac{{na}_{n}}{(2n+1){2}^{n}}$,若b1,bm,bn成等比数列,由等比中项的性质得到
($\frac{m}{2m+1}$)2=$\frac{1}{3}$$•\frac{n}{2n+1}$.由此能求出当且仅当m=2,n=12.使得b1,bm,bn成等比数列.
解答 解:∵an+12=2an2+anan+1,
∴(an+1+an)(2an-an+1)=0,
又an>0,∴2an-an+1=0,即2an=an+1,
∴数列{an}是公比为2的等比数列.
又a1=2.
∴数列{an}的通项公式为an=2n,n∈N*.
∵bn=$\frac{{na}_{n}}{(2n+1){2}^{n}}$=$\frac{n}{2n+1}$,要使b1,bm,bn成等比数列,则(bm)2=b1•bn,($\frac{m}{2m+1}$)2=$\frac{1}{3}$$•\frac{n}{2n+1}$,
得$\frac{{m}^{2}}{4{m}^{2}+4m+1}=\frac{n}{6n+3}$,所以$\frac{3}{n}=\frac{-2{m}^{2}+4m+1}{{m}^{2}}$
∴-2m2+4m+1>0,解得:1-$\frac{\sqrt{6}}{2}$<m<1+$\frac{\sqrt{6}}{2}$.
又m∈N*,且m>1,∴m=2,此时n=12.
故当且仅当m=2,n=12.使得b1,bm,bn成等比数列,此时m+n=14.
故答案为:14
点评 本题考查数列的通项公式的求法、等比中项的性质;关键是由m,n的关系得到关于m的不等式求出m的范围.

练习册系列答案
相关题目
2.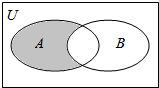 设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
 设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {x|0<x≤1} | D. | {x|x≤1} |
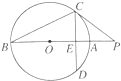 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.