题目内容
【题目】已知函数f（x）是定义域为（0，+∞）的单调函数，若对任意的x∈（0，+∞），都有f[f（x）﹣ 
]=2，则f（2016）=（ ）
A.
B.
C.
D.
【答案】C
【解析】∵f（x）是定义域为（0，+∞）的单调函数，
∴存在唯一的正实数a，使得f（a）=2，
∵对任意的x∈（0，+∞），都有f[f（x）﹣ 
]=2，
∴f（x）﹣ =a，即f（x）= +a，
∵f（a）=2，∴ 
+a=2，得a=1（舍负），
∴f（x）= +1，
∴f（2016）= 
+1= 
．
故选C．
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识，掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．
练习册系列答案
相关题目
【题目】如表提供了甲产品的产量x（吨）与利润y（万元）的几组对照数据．
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程 
= 
x+ 
；
（2）计算相关指数R2的值，并判断线性模型拟合的效果．
参考公式： = 
= 
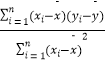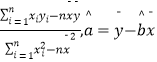，R2=1﹣ 
．
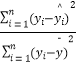