题目内容
等腰三角形ABC中，A=
，AB=AC=2，M是BC的中点，P点在三角形ABC内部或其边界上运动，则
•
的取值范围是（ ）
| π |
| 2 |
| BP |
| AM |
| A、[-1，0] |
| B、[1，2] |
| C、[-2，-1] |
| D、[-2，0] |
分析：根据已知条件建立直角坐标系，以点A为原点，AC所在直线为x轴，AB所在直线为y轴建立如图所示的坐标系，写出点A，B，C，M的坐标，设出点P的坐标，根据点P在三角形ABC内部或其边界上运动，则写出x，y应满足的条件，求出
，
，根据向量的数量积的坐标运算求出
•
，利用线性规划求得它的取值范围．
| BP |
| AM |
| BP |
| AM |
解答：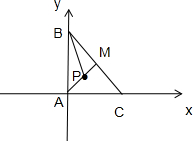
解：以点A为原点，AC所在直线为x轴，AB所在直线为y轴建立如图所示的坐标系，
则A（0，0），B（0，2），C（2，0），设点P（x，y），
∵，M是BC的中点，P点在三角形ABC内部或其边界上运动，
∴M（1，1），
，
=（x，y-2），
=（1，1），
∴
•
=x+y-2，
由图形可知当在点A处取最小值-2，在线段BC上的任意一点取最大值0，
∴
•
的取值范围为[-2，0]．
故选D．
解：以点A为原点，AC所在直线为x轴，AB所在直线为y轴建立如图所示的坐标系，则A（0，0），B（0，2），C（2，0），设点P（x，y），
∵，M是BC的中点，P点在三角形ABC内部或其边界上运动，
∴M（1，1），
|
| BP |
| AM |
∴
| BP |
| AM |
由图形可知当在点A处取最小值-2，在线段BC上的任意一点取最大值0，
∴
| BP |
| AM |
故选D．
点评：此题是个中档题．考查向量在几何中的应用，侧重于对向量坐标运算和数量积、图解法求线性规划问题等基础知识的考查，体现了转化的思想，和熟练应用知识分析、解决问题的能力．
练习册系列答案
相关题目
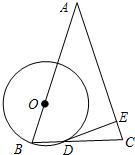如图，在等腰三角形ABC中，AB=AC，O为AB上一点，以O为圆心、OB长为半径的圆交BC于D，DE⊥AC交AC于E．
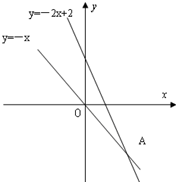已知：等腰三角形ABC中，其中一个腰AC所在的直线方程为y=-2x+2，∠A的平分线所在的直线方程为y=-x，底边BC经过点D（-1，0），求三角形底边BC及腰AB所在的直线方程．
（2013•徐州一模）如图，在等腰三角形ABC中，已知AB=AC=1，A=120°，E，F分别是边AB，AC上的点，且