题目内容
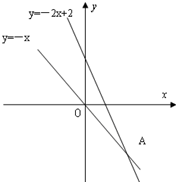 已知:等腰三角形ABC中,其中一个腰AC所在的直线方程为y=-2x+2,∠A的平分线所在的直线方程为y=-x,底边BC经过点D(-1,0),求三角形底边BC及腰AB所在的直线方程.
已知:等腰三角形ABC中,其中一个腰AC所在的直线方程为y=-2x+2,∠A的平分线所在的直线方程为y=-x,底边BC经过点D(-1,0),求三角形底边BC及腰AB所在的直线方程.分析:求出三角形底边BC的斜率,利用点斜式方程求出直线方程,利用P(x,y)直线AB上任意一点,则点P关于∠A的平分线y=-x的对称点(-y,-x)在腰AC所在的直线上,求出直线方程.
解答:解:在等腰三角形ABC中,顶角A的平分线y=-x垂直于底边BC
∴底边BC所在的直线斜率kBC=1…(3分)
又直线过点D(-1,0)
∴由点斜式得到底边BC所在的直线方程为y=x+1…(6分)
腰AB的所在的直线方程解法如下:
设P(x,y)直线AB上任意一点,则点P关于∠A的平分线y=-x的对称点(-y,-x)在腰AC所在的直线上…(9分)
将(-y,-x)代入方程y=-2x+2得-x=-2(-y)+2
化简得腰AB所在的直线方程 x+2y+2=0…(12分)
∴底边BC所在的直线斜率kBC=1…(3分)
又直线过点D(-1,0)
∴由点斜式得到底边BC所在的直线方程为y=x+1…(6分)
腰AB的所在的直线方程解法如下:
设P(x,y)直线AB上任意一点,则点P关于∠A的平分线y=-x的对称点(-y,-x)在腰AC所在的直线上…(9分)
将(-y,-x)代入方程y=-2x+2得-x=-2(-y)+2
化简得腰AB所在的直线方程 x+2y+2=0…(12分)
点评:本题考查直线方程的求法,考查直线的垂直以及对称问题的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
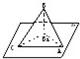 如图,已知一个等腰三角形ABC的顶角B=120°,过AC的一个平面α与顶点B的距离为1,根据已知条件,你能求出AB在平面α上的射影AB1的长吗?如果不能,那么需要增加什么条件,可以使AB1=2?
如图,已知一个等腰三角形ABC的顶角B=120°,过AC的一个平面α与顶点B的距离为1,根据已知条件,你能求出AB在平面α上的射影AB1的长吗?如果不能,那么需要增加什么条件,可以使AB1=2?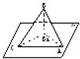 如图,已知一个等腰三角形ABC的顶角B=120°,过AC的一个平面α与顶点B的距离为1,根据已知条件,你能求出AB在平面α上的射影AB1的长吗?如果不能,那么需要增加什么条件,可以使AB1=2?
如图,已知一个等腰三角形ABC的顶角B=120°,过AC的一个平面α与顶点B的距离为1,根据已知条件,你能求出AB在平面α上的射影AB1的长吗?如果不能,那么需要增加什么条件,可以使AB1=2?