题目内容
已知命题P:函数y=loga(1-2x)在定义域上单调递增;命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若P∨Q是真命题,求实数a的取值范围.
(-2,2]
解:命题P:函数y=loga(1-2x)在定义域上单调递增,
∴0<a<1.
又∵命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立,
∴a=2或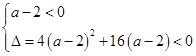
即-2<a≤2.
∵P∨Q是真命题,
∴a的取值范围是(-2,2].
∴0<a<1.
又∵命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立,
∴a=2或
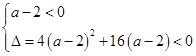
即-2<a≤2.
∵P∨Q是真命题,
∴a的取值范围是(-2,2].

练习册系列答案
相关题目
 :“若
:“若 ,则
,则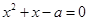 有实根”.
有实根”.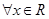 ,
, ”是全称命题;
”是全称命题;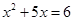 ”的否定是“
”的否定是“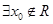 ,使
,使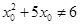 ”;
”;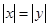 ,则
,则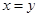 ;
; 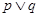 为假命题,则
为假命题,则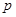 、
、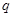 均为假命题.
均为假命题.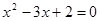 ,则
,则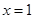 ”的逆否命题为“若
”的逆否命题为“若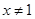 ,则
,则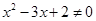 ”
”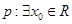 ,使得
,使得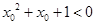 ,则
,则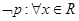 ,则
,则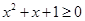
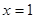 ”是“
”是“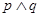 为假命题,则
为假命题,则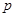 、
、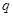 均为假命题
均为假命题 p是假命题,则实数m的取值范围是( )
p是假命题,则实数m的取值范围是( )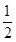 >0.则命题“p∧(
>0.则命题“p∧( q)”是假命题;
q)”是假命题;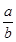 =-3;
=-3;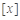 表示不超过
表示不超过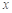 的最大整数,如
的最大整数,如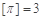 ,
,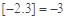 .给出下列命题:
.给出下列命题: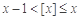 ;
;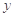 ,都有
,都有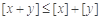 ;③
;③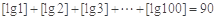 ;
;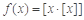 ,当
,当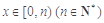 时,令
时,令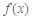 的值域为A,记集合A的元素个数为
的值域为A,记集合A的元素个数为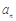 ,则
,则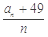 的最小值为
的最小值为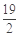 .
.