题目内容

20．对于平面直角坐标系中任意两点P（x1，y1），Q（x2，y2），我们将|x1-x2|+|y1-y2|定义为PQ两点的“耿直距离”．已知A（0，0），B（3，1），C（4，4），D（1，3），设M（x，y）是平面直角坐标系中的一个动点．若使得点M到A、B、C、D的“耿直距离”之和取得最小值，则点M应位于下列哪个图中的阴影区域之内．（　　）
A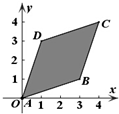．B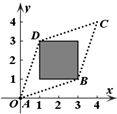．C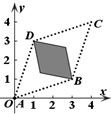．D．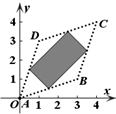

分析 通过所求图形，求出最小值，利用特殊点求解点M到A、B、C、D的“耿直距离”之和判断即可．

解答 解：由题意可知M（2，2）满足椭圆，点M到A、B、C、D的“耿直距离”之和为：12．
当M（1，1）时，点M到A、B、C、D的“耿直距离”之和为12．排除C，
当M（0，0）时，点M到A、B、C、D的“耿直距离”之和为16．排除A，
当M（1，3）时，点M到A、B、C、D的“耿直距离”之和为12．排除D，
故选：B．

点评 本题考查新定义的应用，特殊法求解选择题的方法，考查计算能力，分析问题解决问题的能力．

练习册系列答案
相关题目
9．若（2x-1）4=a0+a1x+a2x2+a3x3+a4x4，则a0+a2+a4=（　　）
A．-119B．-120C．-121D．41
11．已知椭圆M：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1，过点P（1，2）的直线l与x，y轴正半轴围成的三角形面积最小时，l恰好经过曲线M的两个顶点A，B．
（1）求椭圆M的方程；
（2）直线l交曲线M于点C，D（异于A，B）两点，求四边形ABCD面积最大时，直线l的方程．
8．已知函数f（x）=sinxcosxcosφ+cos2xsinφ+$\frac{1}{2}$sin（π+φ）（0＜φ＜π），其图象过点（$\frac{π}{4}，\frac{1}{4}$）
（Ⅰ）求φ的值；
（Ⅱ）将函数y=f（x）图象向右平移$\frac{π}{12}$个单位长度，得到函数y=g（x）的图象，求函数g（x）在[0，π]上的单调增区间．
15．过点A（2，-4）且与直线2x-y+3=0平行的直线方程为（　　）
A．x+2y-8=0B．2x-y-8=0C．x+2y-4=0D．2x-y=0
5．命题“对任意x∈R，都有x2＜0”的否定为（　　）
A．对任意x∈R，都有x2≤0B．不存在x∈R，使得x2＜0
C．存在x0∈R，使得x02≥0D．存在x0∈R，使得x02＜0
12．已知圆C：（x-1）2+（y-1）2=9，直线l：（2m+1）x+（m+1）y-7m-4=0（m∈R）
（1）若m=0，求直线被圆C截得的弦长；
（2）证明：不论m取什么实数，直线l与圆恒交于两点．
9．命题“若x2＜1，则-1＜x＜1”的否命题是（　　）
A．若x2≥1，则x≥1或x≤-1B．若-1＜x＜1，则x2＜1
C．若x≥1或x≤-1，则x2≥1D．若x≥1且x≤-1，则x2≥1
10．在△ABC中，BC=2，B=$\frac{π}{3}$，若△ABC的面积为$\frac{\sqrt{3}}{2}$，则AC=$\sqrt{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网