题目内容
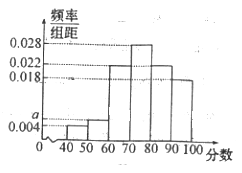
【题目】语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:

(I)如果成绩大于135的为特别优秀,这500名学生中本次考试语文、数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布的)
(II)如果语文和数学两科都特别优秀的共有6人,从(I)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
,![]() .
.
【答案】(I)语文![]() 人,数学
人,数学![]() 人;(II)分布列见解析,
人;(II)分布列见解析,![]() .
.
【解析】
试题分析:(I)根据正态分布的知识,可分别求得语文特别优秀与数学特别优秀的概率,由此可求得特别优秀语文、数学的人数;(II)首先求得![]() 所有可能的取值,然后分别求得相应概率,由此列出分布列,求出期望.
所有可能的取值,然后分别求得相应概率,由此列出分布列,求出期望.
试题解析:(I)语文成绩特别优秀的概率为![]() ,………………1分
,………………1分
数学成绩特别优秀的概率为![]() ,………………3分
,………………3分
语文成绩特别优秀人数为![]() 人,
人,
数学成绩特别优秀人数为![]() 人.……………………5分
人.……………………5分
(II)语文数学两科都优秀的6人,单科优秀的有10人,
![]() 所有可能的取值为0,1,2,3.
所有可能的取值为0,1,2,3.
![]() ,
,![]() ,
,
![]() ,
,![]() ,………………10分
,………………10分
分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
………………11分
数学期望![]() .………………12分
.………………12分

练习册系列答案
相关题目