Question

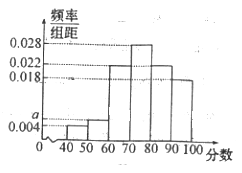
【题目】某学校为了解学校食堂的服务情况，随机调查了50名就餐的教师和学生.根据这50名师生对餐厅服务质量进行评分，绘制出了频率分布直方图（如图所示），其中样本数据分组为.

（1）求频率分布直方图中的值；

（2）从评分在的师生中，随机抽取2人，求此人中恰好有1人评分在上的概率；

（3）学校规定：师生对食堂服务质量的评分不得低于75分，否则将进行内部整顿，试用组中数据估计该校师生对食堂服务质量评分的平均分，并据此回答食堂是否需要进行内部整顿.

Answer 1

【答案】（1）0.006（2） （3）76.2,不需要内部整顿.

【解析】试题分析：

(1)由频率分布直方图小长方形面积之和为1可得关于实数a的方程，解方程可得 ；

(2)利用题意列出所有可能的结果，由古典概型公式可得此人中恰好有1人评分在上的概率为

(3)求解平均值 可知食堂不需要内部整顿.

试题解析：

（1）由 ,

得 .

（2）设被抽取的2人中恰好有一人评分在上为事件A.

因为样本中评分在的师生人数为：，记为1,2号

样本中评分在的师生人数为：，记为3,4,5号

所以从5人中任意取2人共有（1,2），（1,3），（1,4），（1,5），（2,3），（2,4），（2,5），（3,4），（3,5），（4,5）共10种等可能情况；2人中恰有1人评分在上有（1,3），（1,4），（1,5），（2,3），（2,4），（2,5）共6种等可能情况.

得 .

答：2人中恰好有1人评分在上的概率为.

(3) 服务质量评分的平均分为

因为 , 所以食堂不需要内部整顿.