题目内容
8.化简:(x${\;}^{\frac{a+b}{c-a}}$)${\;}^{\frac{1}{b-c}}$•(x${\;}^{\frac{c+a}{b-c}}$)${\;}^{\frac{1}{a-b}}$•(x${\;}^{\frac{b+c}{a-b}}$)${\;}^{\frac{1}{c-a}}$.分析 利用指数幂的运算性质、通过通分化简整理即可得出.
解答 解:原式=${x}^{\frac{a+b}{c-a}×\frac{1}{b-c}+\frac{c+a}{b-c}×\frac{1}{a-b}+\frac{b+c}{a-b}×\frac{1}{c-a}}$
=${x}^{\frac{(a+b)(a-b)+(c+a)(c-a)+(b+c)(b-c)}{(c-a)(b-c)(a-b)}}$
=x0
=1.
点评 本题考查了指数幂的运算性质、通分方法,考查了计算能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
7.曲线C以双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}$=1的右焦点F为焦点,曲线C上的点到焦点F的距离与到直线x=-2的距离相等,则曲线C上的任意一点P到y轴的距离与到直线x-y+4=0的距离和的最小值为( )
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{2}$-1 | C. | 3$\sqrt{2}$+2 | D. | 3$\sqrt{2}$-2 |
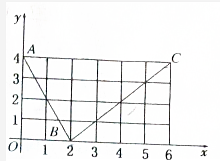 如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).
如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).