题目内容
5.已知P(-1,1),Q(2,2),若直线l:y=mx-1与射线PQ(P为端点)有交点,则实数m的取值范围是m≤-2或m>$\frac{1}{3}$.分析 利用直线l:y=mx-1与经过定点,A(0,-1),求得直线AQ的斜率kAQ,直线AP的斜率kAP即可得答案.
解答 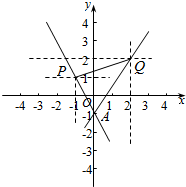 解:∵直线l:y=mx-1与恒过定点A(0,-1),线段PQ两端点的坐标分别为P(-1,1)和Q(2,2),
解:∵直线l:y=mx-1与恒过定点A(0,-1),线段PQ两端点的坐标分别为P(-1,1)和Q(2,2),
∴直线AQ的斜率kAQ=$\frac{3}{2}$,直线AP的斜率kAP=-2,kPQ=$\frac{1}{3}$,
依题意有:m≤-2或m>$\frac{1}{3}$.
故答案为:m≤-2或m>$\frac{1}{3}$.
点评 本题考查:两条直线的交点坐标,考查恒过定点的直线,考查直线的斜率的应用,考查作图与识图能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13.在△ABC中,∠A=90°,$\overrightarrow{AB}$=(k,1),$\overrightarrow{AC}$=(2,3),则k的值是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
14.已知x、y满足y=3-$\sqrt{4x-{x}^{2}}$,则使x+2y+2a<0恒成立的a的取值范围是( )
| A. | [$\sqrt{5}-4$,$\sqrt{5}+4$] | B. | (-∞,-5] | C. | [-5,+∞) | D. | (-∞,-5) |
15.函数y=lg(x-1)+lg(x-2)的定义域为M,函数y=lg(x2-3x+2)的定义域为N,则 ( )
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |