题目内容
17.已知f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,0<|φ|<$\frac{π}{2}$),f(0)=0,且函数f(x)图象上的任意两条对称轴之间距离的最小值是$\frac{π}{2}$.(1)求f($\frac{π}{8}$)的值;
(2)将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位后,得到函数y=g(x)的图象,求函数g(x)的解析式,并求g(x)在x∈[$\frac{π}{6}$,$\frac{π}{2}$]上的最值.
分析 (1)由条件利用两角和差的正弦公式化简f(x)的解析式,由周期求出ω,由f(0)=0求出φ的值,可得f(x)的解析式,从而求得f($\frac{π}{8}$)的值.
(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再根据正弦函数的定义域和值域求得g(x)在x∈[$\frac{π}{6}$,$\frac{π}{2}$]上的最值.
解答 解:(1)f(x)=sin(ωx+φ)+cos(ωx+φ)=$\sqrt{2}$sin(ωx+φ+$\frac{π}{4}$),
故 $\frac{2π}{ω}$=2×$\frac{π}{2}$,求得ω=2.
再根据f(0)=sin(φ+$\frac{π}{4}$)=0,0<|φ|<$\frac{π}{2}$,可得φ=-$\frac{π}{4}$,
故 f(x)=$\sqrt{2}$sin2x,f($\frac{π}{8}$)=$\sqrt{2}$sin$\frac{π}{4}$=1.
(2)将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位后,得到函数y=g(x)=$\sqrt{2}$sin2(x-$\frac{π}{6}$)=$\sqrt{2}$sin(2x-$\frac{π}{3}$)的图象.
∵x∈[$\frac{π}{6}$,$\frac{π}{2}$],∴2x-$\frac{π}{3}$∈[0,$\frac{2π}{3}$],当2x-$\frac{π}{3}$=$\frac{π}{2}$时,g(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$)取得最大值为$\sqrt{2}$;
当2x-$\frac{π}{3}$=0时,g(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$)取得最小值为0.
点评 本题主要考查两角和差的正弦公式,由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由f(0)=0求出φ的值,可得f(x)的解析式;函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于中档题.

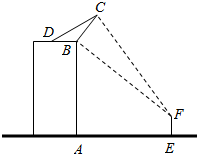 如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.
如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.