题目内容
16.已知圆O:x2+y2=1及点A(2,0),点P(x0,y0)(y0≠0)是圆O上的动点,若∠OPA<60°,则x0的取值范围是(-1,$\frac{3-\sqrt{13}}{8}$).分析 考虑当∠OPA=60°时,x0的取值,即可得出结论.
解答 解:当∠OPA=60°时,设AP=x,则
由余弦定理可得4=1+x2+2×$1×x×\frac{1}{2}$,
∴x=$\frac{-1+\sqrt{13}}{2}$,
∴S△OPA=$\frac{1}{2}×1×$$\frac{-1+\sqrt{13}}{2}$=$\frac{-1+\sqrt{13}}{4}$.
由等面积可得|y0|=$\frac{-1+\sqrt{13}}{4}$,
∴x0=$\frac{3-\sqrt{13}}{8}$(正数舍去),
∵∠OPA<60°,
∴x0的取值范围是(-1,$\frac{3-\sqrt{13}}{8}$).
故答案为:(-1,$\frac{3-\sqrt{13}}{8}$).
点评 本题考查直线与圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
4.命题p:?x∈R,x2+ax+a2≥0;命题q:若一条直线不在平面内,则这条直线就与这个平面平行,则下列命题中为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | (¬p)∧(¬q) |
11.如图所示,程序框图(算法流程图)输出的结果是( )
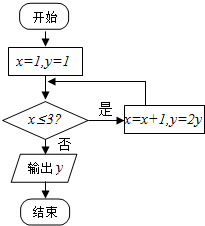

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |