题目内容
一块形状为直角三角形的铁皮，直角边长分别为40cm和60cm，现要将它剪成一个矩形，并以此三角形的直角为矩形的一个角，问：怎样剪，才能使剩下的残料最少?
当x=30时，S取得最小值为600，此时y=20
解析在直角三角形铁皮ABC中，剪出一个矩形CDEF。设CD=x,CF=y,则AF=40-y.
因为△AEF∽△ABC，所以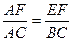 
即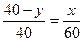 
所以 
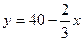…………5分
剩下残料的面积：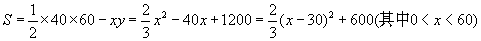
……9分
所以，当x=30时，S取得最小值为600，此时y=20
故在直角三角形铁皮的两直角边中点处剪开时，剩下的残料最少，最少残料600cm2…12分
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
是定义在
上的偶函数，当
时，
为实数）.
时，求
，试判断
上的单调性，并证明你的结论；
，使得当
有最大值1？若存在，求出
的最大值和最小正周期； 
三个内角，若，
，且C为锐角，求
（x∈R），Ｐ1（ｘ1，ｙ1），Ｐ2（ｘ2，ｙ2）是函数ｙ＝ｆ(x)图像上两点，且线段Ｐ1Ｐ2中点Ｐ的横坐标为
。
｝的通项公式为
)(ｍ∈Ｎ
，ｎ＝１,２,３,…,ｍ），求数列｛
； （5分）
＜
横成立，求实数a的取值范围。（3分）
．
在点
处与直线
相切，求
的值；
的单调区
间与极值点．
是同时满足下列两个性质的函数
组成的集合：
，使得
．
是否属于集合
，求实数
的取值范围．
,求:
;(2)
;(3)函数
.
的导函数
，
，
、
为实数。
，
）处切线的斜率为12，求
，求函数
是定义在
上的减函数，并且满足
，
，
,
,
的值， （2）如果
，求x的取值范围。