题目内容
【题目】设椭圆
的焦点
,过右焦点
的直线
与
相交于
两点，若
的周长为短轴长的
倍.
（1）求
的离心率;
（2）设
的斜率为
，在上是否存在一点
,使得
？若存在，求出点的坐标; 若不存在，说明理由.
【答案】（1）
（2）不存在
【解析】
试题分析：（1）求椭圆离心率，只需建立一个等量关系即可：因为
的周长为
，所以
，注意短轴长为
，即可得到
（2）存在性问题，以算代证，有解就存在，无解就不存在. 设
，
，则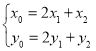
，代入椭圆方程为
化简得
，再根据直线方程
与椭圆方程联立方程组，利用韦达定理得
，计算 
，则与矛盾，故不存在
试题解析：（1）
的周长为，依题意知，即 
.
（2）设椭圆方程为，直线的方程为，代入椭圆方程得
，
设，则,设，则
①
由
得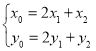,代入① 得
,
因为
②
而,从而 ②式不成立. 故不存在点
，使
成立.
练习册系列答案
相关题目
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒, 以防止害虫的危害, 但采集上市时蔬菜仍存有少量的残留农药, 食用时需要用清水清洗干净, 下表是用清水
(单位：千克) 清洗该蔬菜
千克后, 蔬菜上残留的农药
(单位：微克) 的统计表：
|
|
|
|
|
|
|
|
|
|
|
|
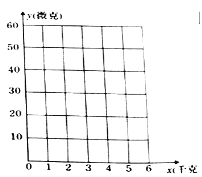
（1）在下面的坐标系中, 描出散点图, 并判断变量
与
的相关性；
（2）若用解析式
作为蔬菜农药残量
与用水量的回归方程, 令
,计算平均值
与
,完成以下表格(填在答题卡中) ,求出与的回归方程.(
精确到
)
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
（3）对于某种残留在蔬菜上的农药,当它的残留量低于
微克时对人体无害, 为了放心食用该蔬菜, 请
估计需要用多少千克的清水清洗一千克蔬菜？(精确到,参考数据
)
(附：线性回归方程
中系数计算公式分别为；
, 
)
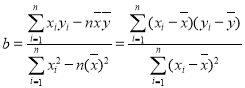