题目内容
某企业要建造一个容积为18m3,深为2m的长方体形无盖贮水池,如果池底和池壁每平方米的造价分别为200元和150元,怎样设计该水池可使得能总造价最低?最低总造价为多少?
将水池的地面设计成边长为3m的正方形时总造价最低,最低总造价为5400元.
解析试题分析:
解题思路:设出未知量,根据容积为18,得出未知量间的关系,列出函数表达式,利用基本不等式进行求最值.
规律总结:解决数学应用题的步骤:①审题,设出有关量,注明自变量的取值范围;②列出函数表达式;③求函数的最值;④作答.
试题解析:设底面的长为xm,宽为ym,水池总造价为z元,
则由容积为18m3,可得:2xy=16,因此xy=9,
z=200×9+150(2×2x+2×2y)=1800+600(x+y)≥1800+600•2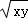 =5400
=5400
当且仅当x=y=3时,取等号.
所以,将水池的地面设计成边长为3m的正方形时总造价最低,最低总造价为5400元.
考点:基本不等式.

练习册系列答案
相关题目
 满足
满足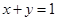 ,求
,求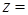
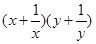 的最小值.
的最小值.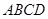 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中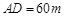 ,
,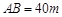 ,且
,且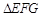 中,
中, ,经测量得到
,经测量得到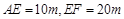 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点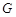 作一直线交
作一直线交 于
于 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设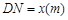 .
.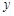 表示为
表示为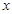 的函数;
的函数; 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.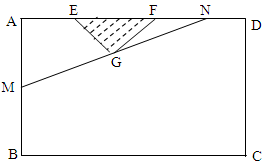
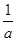 -1)(
-1)(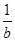 -1)(
-1)(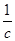 -1)≥8.
-1)≥8.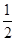 AB,tan∠FED=
AB,tan∠FED=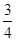 ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.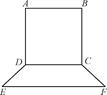
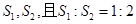 ,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.
,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.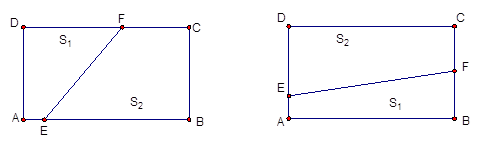
 ,则函数
,则函数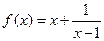 的最小值为 .
的最小值为 .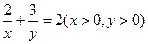 ,则
,则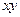 的最小值是__ ▲ __.
的最小值是__ ▲ __.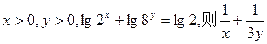 的最小值是 。
的最小值是 。