题目内容
已知两正数 满足
满足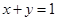 ,求
,求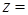
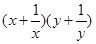 的最小值.
的最小值.
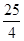 .
.
解析试题分析:首先将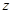 变形为
变形为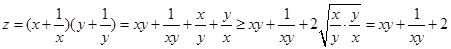 ,而
,而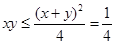 ,因此对于
,因此对于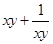 不能用基本不等式
不能用基本不等式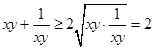 (当
(当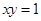 时“=”成立),∴可以考虑函数
时“=”成立),∴可以考虑函数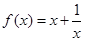 在
在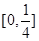 上的单调性,易得
上的单调性,易得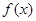 在
在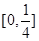 上是单调递减的,故
上是单调递减的,故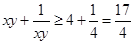 ,∴
,∴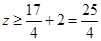 ,当且仅当
,当且仅当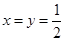 时,“=”成立,即
时,“=”成立,即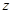 的最小值为
的最小值为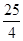 .
.
试题解析: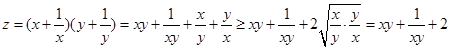 ,∵
,∵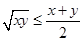 ,
,
∴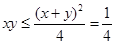 ,构造函数
,构造函数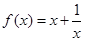 ,易证
,易证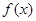 在
在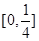 上是单调递减的,∴.
上是单调递减的,∴.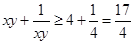 ,∴
,∴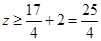 ,当且仅当
,当且仅当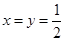 时,“=”成立,∴
时,“=”成立,∴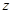 的最小值为
的最小值为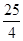 .
.
考点:1.基本不等式求最值;2.函数的单调性求最值.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

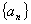 中,
中,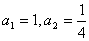 ,且
,且 .
.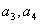 ,猜想
,猜想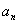 的表达式,并加以证明;
的表达式,并加以证明;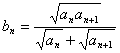 ,求证:对任意的自然数
,求证:对任意的自然数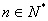 都有
都有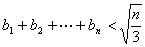 .
. 的最大值为
的最大值为 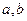 满足
满足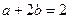 ,则
,则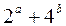 的最小值为__________.
的最小值为__________.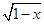 +
+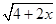 的最大值.
的最大值.