Question

【题目】设是大于1的自然数，找出所有自然数，使得对于存在互质的自然数、，满足.

Answer 1

【答案】

【解析】

先证明一个引理.

引理 设、、、、，且满足.若是大于1的奇数， 是奇质数，则可以表示成的以自然数为指数的幂.

引理的证明：设为、的最大公约数，可设.由已知条件有.

因此，存在某个非负整数，满足.

由于是奇数，故有.

用表示等式右端的数.由于，所以，与中至少有一个大于1.而，因此，.由式①推出.

因为且，所以，它们都能被整除，且存在某个自然数，使得.这样，

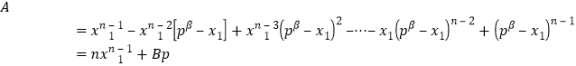（是某个整数）.

因为，且，于是.

设，则，即.

如果，同上面证明一样，可以证明可被整除.如果，则；这样重复下去，便可推出，存在某个自然数，有.

下面证明本题的结论：的可能值只有2.

设，其中，不妨设.由于，，显然且.讨论如下：

（1）若是偶数，则.

于是，不是3的整数次幂，矛盾.

（2）若是奇数，且，则.于是，.以下证明.

由引理知.取，代入后，可以认为.于是，，即证明.

由于，则.

因此，.

于是，得证.

由，推出.

而且. ②

如果②中至少有一个不等号是严格不等号，那么，.由推出矛盾.可见，.

那么，，且.故是惟一满足条件的值.