题目内容
【题目】在一个![]() 的方格表的每个方格内填入1或
的方格表的每个方格内填入1或![]() ,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
【答案】1
【解析】
假设存在某种成功填法,其中含有![]() .
.
首先证明:若此种成功填法关于中间一列(行)对称,则中间一列(行)全为1.
设![]() ,
,![]() .若
.若![]() ,由
,由![]() ,得
,得![]() .
.
同理,![]() ,…,
,…,![]() .
.
若![]() ,同理可得
,同理可得![]() .
.
因此,若![]() ,则
,则![]() .这样,
.这样,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() .从而
.从而![]() ,矛盾.
,矛盾.
因此,中间一列(行)全为1.
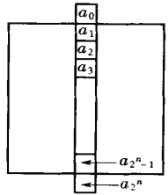
其次,若此种成功填法不关于中间一列对称,先将此种填法沿中间一列翻转![]() ,得另一种填法,再将两种填法处于相同位置的数相乘,就得到关于中间一列对称的成功填法,其中含有
,得另一种填法,再将两种填法处于相同位置的数相乘,就得到关于中间一列对称的成功填法,其中含有![]() .此种成功填法可进一步转化为既关于中间一行,又关于中间一列对称的成功填法,其中含有
.此种成功填法可进一步转化为既关于中间一行,又关于中间一列对称的成功填法,其中含有![]() .
.
对这样的![]() 的成功填法,去掉中间一行与中间一列的所有1,就可得到4个
的成功填法,去掉中间一行与中间一列的所有1,就可得到4个![]() 的成功填法,至少有一个其中含有
的成功填法,至少有一个其中含有![]() .对这个成功填法,一直重复上面的操作,最终可得到一个
.对这个成功填法,一直重复上面的操作,最终可得到一个![]() 的成功填法,其中含有
的成功填法,其中含有![]() ,但中间一行和中间一列全为1,这与成功填法的定义矛盾.
,但中间一行和中间一列全为1,这与成功填法的定义矛盾.
因此,对任意成功填法,其中一定不含有![]() .故成功填法只有1种,即每个方格中均填1.
.故成功填法只有1种,即每个方格中均填1.

【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
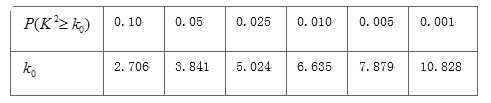
附: (其中
(其中![]() )和临界值表:
)和临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.45 | 0.708 | 1.32 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |