Question

（2010•和平区一模）如图，在直三棱柱ABC-A₁B₁C₁中，已知AA₁=2，AC=BC=1，且AC⊥BC，M是A₁B₁的中点．
（Ⅰ）求证：CB₁∥平面AC₁M；
（Ⅱ）设AC与平面AC₁M的夹角为θ，求sinθ．

Answer 1

分析：（I）分别以CA、CB、CC₁为x、y、z轴，建立空间直角坐标系C-xyz，可得C、C₁、A、B₁、A₁各点的坐标，从而算出

AM

、

C1M

和

CB1

的坐标，证出

CB1

=

AM

+

C1M

，结合CB₁?平面AC₁M，即可证出CB₁∥平面AC₁M；
（II）利用垂直向量数量积为零的方法，建立方程组解出向量

n

=（2，-2，1）为平面AC₁M的一个法向量，根据空间向量的夹角公式算出

n

与

AC

夹角的余弦，结合直线与平面所成角的性质即可得出sinθ=|cos＜

n

，

AC

＞|=

2

3

．

解答：解：（I）因为CA、CB、CC₁两两互相垂直，所以分别以CA、CB、CC₁为x、y、z轴，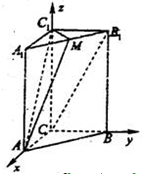
建立空间直角坐标系C-xyz，如图所示
则C（0，0，0），C₁（0，0，2），A（1，0，0），B₁（0，1，2），A₁（1，0，2），
∵M是A₁B₁的中点，∴M（

1

2

，

1

2

，2）
由此可得，

AM

=（-

1

2

，

1

2

，2），

C1M

=（

1

2

，

1

2

，0），

CB1

=（0，1，2），
∴

CB1

=

AM

+

C1M

，可得

CB1

∥平面AC₁M
∵CB₁?平面AC₁M，∴CB₁∥平面AC₁M；
（II）设向量

n

=（x，y，z）为平面AC₁M的一个法向量
则

n • C1M = 1 2 x+ 1 2 y=0 n • AM =- 1 2 x+ 1 2 y+2z=0

，取z=1，得x=2，y=-2，
∴

n

=（2，-2，1）为平面AC₁M的一个法向量
∵

AC

=（-1，0，0），
∴cos＜

n

，

AC

＞=

2×(-1)+(-2)×0+1×0

22+(-2)2+12 • (-1)2+02+02

=

2

3

∵AC与平面AC₁M的夹角为θ，∴sinθ=|cos＜

n

，

AC

＞|=

2

3

点评：本题在特殊的三棱柱中证明线面平行，并求直线与平面所成角的正弦之值，着重考查了利用空间坐标系的方法求空间角和线面平行的判定定理等知识，属于中档题．