题目内容
在棱长为a的正方体ABCD—A′B′C′D′中,E、F分别是BC、A′D′的中点![]()
(1)求直线A′C与DE所成的角;
(2)求直线AD与平面B′EDF所成的角;
(3)求面B′EDF与面ABCD所成的角![]()
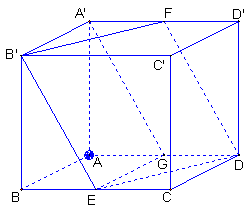
(1)解![]() 如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角![]()
 在△A′CP中,易得A′C=
在△A′CP中,易得A′C=![]() a,CP=DE=
a,CP=DE=![]() a,A′P=
a,A′P=![]() a
a
由余弦定理得cosA′CP=![]()
故A′C与DE所成角为arccos![]()
![]()
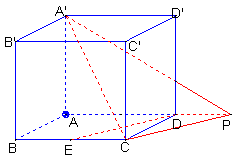
(2)解![]() ∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上(如图)又可证明四边形B′EDF为菱形(证明略),∴DB′为∠EDF的平分线,
∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上(如图)又可证明四边形B′EDF为菱形(证明略),∴DB′为∠EDF的平分线,
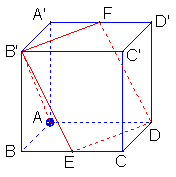 故直线AD与平面B′EDF所成的角为∠ADB′,
故直线AD与平面B′EDF所成的角为∠ADB′,
在Rt△B′AD中,AD=![]() a,AB′=
a,AB′=![]() a,B′D=
a,B′D=![]() a,
a,
则cosADB′=![]() ,故AD与平面B′EDF所成的角是arccos
,故AD与平面B′EDF所成的角是arccos![]()
![]()
 (3)解
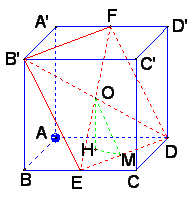
(3)解![]() 如图,连结EF、B′D,交于O点,显然O为B′D的中点,从而O为正方形ABCD—A′B′C′D的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心,再作HM⊥DE,垂足为M,连结OM,则OM⊥DE,故∠OMH为二面角B′—DE′—A的平面角
如图,连结EF、B′D,交于O点,显然O为B′D的中点,从而O为正方形ABCD—A′B′C′D的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心,再作HM⊥DE,垂足为M,连结OM,则OM⊥DE,故∠OMH为二面角B′—DE′—A的平面角![]()
在Rt△DOE中,OE=![]() a,OD=
a,OD=![]() a,斜边DE=
a,斜边DE=![]() a,
a,
则由面积关系得OM=![]() a
a
在Rt△OHM中,sinOMH=![]()
故面B′EDF与面ABCD所成的角为arcsin![]()
![]()
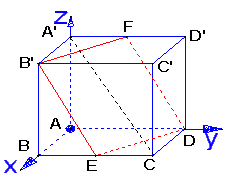
方法二(向量法)![]()
(1) 如图建立坐标系,则![]()
![]()
![]()
故A′C与DE所成角为arccos![]()
![]()
(2)∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上![]() 如下图所示
如下图所示![]() 又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′,如图建立坐标系,则
![]()
![]()
 ,
,
故AD与平面B′EDF所成的角是arccos![]()
![]()
(3) 由(1)知![]() ,
,
所以面ABCD的法向量为![]()
![]() 下面求面B′EDF的法向量
下面求面B′EDF的法向量![]()
![]()
设![]() ,由
,由![]()
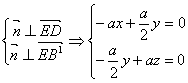
取z=1,得![]()
![]() ∴
∴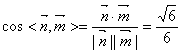 .
.
故面B′EDF与面ABCD所成的角为![]()
![]()
解析:
求线面角关键是作垂线,找射影,求异面直线所成的角采用平移法![]() 求二面角的大小也可应用面积射影法
求二面角的大小也可应用面积射影法![]() 点评:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强
点评:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强![]() 用平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角,是常用的方法.
用平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角,是常用的方法.


