题目内容
已知a>b>0F是方程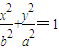 的椭圆E的一个焦点,P、A,B是椭圆E上的点,
的椭圆E的一个焦点,P、A,B是椭圆E上的点,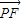 与x轴平行,
与x轴平行,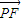 =
=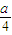 ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),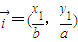 ,
,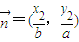 ,
,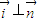 原点O与A、B两点构成的△AOB的面积为S
原点O与A、B两点构成的△AOB的面积为S(I )求椭圆E的离心率
(II)设椭圆E上的点与椭圆£的长轴的两个端点构成的三角形的面积的最大值等于2,S是否为定值?如果是,求出这个定值:如果不是,请说明理由.
【答案】分析:(I )由a>b>0,P是椭圆E上的点,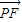 与x轴平行,知
与x轴平行,知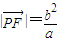 ,由
,由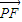 =
= ,知
,知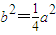 ,由此能求出离心率.
,由此能求出离心率.
(II)由题设知椭圆E的方程为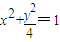 ,若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),由
,若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),由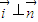 ,知y1=±2x1.S=
,知y1=±2x1.S=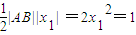 .当直线AB的斜率存在时,设直线AB为:kx-y+m=0,设A(x1,kx1+m),B(x2,kx2+m),则
.当直线AB的斜率存在时,设直线AB为:kx-y+m=0,设A(x1,kx1+m),B(x2,kx2+m),则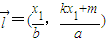 ,
, ,由
,由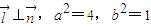 ,知
,知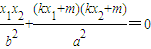 ,由
,由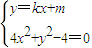 ,得(4+k2)x2+2kmx+m2-4=0,再由韦达定理进行求解.
,得(4+k2)x2+2kmx+m2-4=0,再由韦达定理进行求解.
解答:解:(I )∵a>b>0,P是椭圆E上的点,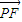 与x轴平行,
与x轴平行,
∴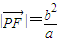 ,
,
∵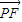 =
=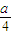 ,
,
∴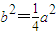 ,
,
∴ ,
,
∴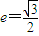 .
.
(II)∵椭圆E上的点与椭圆E的长轴的两个端点构成的三角形的面积的最大值等于2,
∴ab=2,解方程组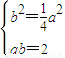 ,得
,得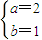 ,
,
∴椭圆E的方程为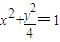 .
.
若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),
∵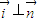 ,
,
∴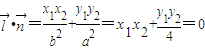 ,
,
即y1=±2x1.
此时S=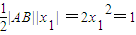 .
.
当直线AB的斜率存在时,设直线AB为:kx-y+m=0,
设A(x1,kx1+m),B(x2,kx2+m),
则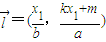 ,
,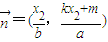 ,
,
∵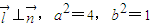 ,
,
∴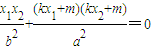 ,
,
即(4+k2)x1x2+mk(x1+x2)+m2=0x1x2+mk(x1+x2)+m2=0,
由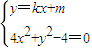 ,得(4+k2)x2+2kmx+m2-4=0,
,得(4+k2)x2+2kmx+m2-4=0,
∴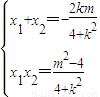 ,
,
∴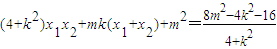 ,
,
∵(4+k2)x1x2+mk(x1+x2)+m2=0,
∴8m2-4k2-16=0,即mk(x1+x2)+m2=0.
∵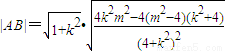
=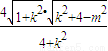
=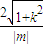 .
.
原点O到kx-y+m=0的距离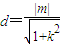 ,
,
∴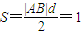 .
.
综上所述,△AOB的面积是定值,等于1.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用韦达定理、点到直线距离公式,注意合理地进行等价转化.
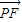 与x轴平行,知
与x轴平行,知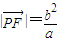 ,由
,由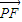 =
= ,知
,知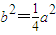 ,由此能求出离心率.
,由此能求出离心率.(II)由题设知椭圆E的方程为
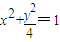 ,若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),由
,若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),由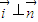 ,知y1=±2x1.S=
,知y1=±2x1.S=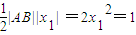 .当直线AB的斜率存在时,设直线AB为:kx-y+m=0,设A(x1,kx1+m),B(x2,kx2+m),则
.当直线AB的斜率存在时,设直线AB为:kx-y+m=0,设A(x1,kx1+m),B(x2,kx2+m),则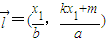 ,
, ,由
,由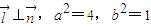 ,知
,知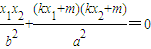 ,由
,由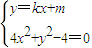 ,得(4+k2)x2+2kmx+m2-4=0,再由韦达定理进行求解.
,得(4+k2)x2+2kmx+m2-4=0,再由韦达定理进行求解.解答:解:(I )∵a>b>0,P是椭圆E上的点,
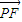 与x轴平行,
与x轴平行,∴
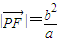 ,
,∵
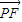 =
=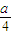 ,
,∴
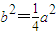 ,
,∴
 ,
,∴
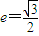 .
.(II)∵椭圆E上的点与椭圆E的长轴的两个端点构成的三角形的面积的最大值等于2,
∴ab=2,解方程组
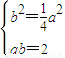 ,得
,得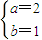 ,
,∴椭圆E的方程为
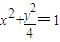 .
.若直线AB与x轴垂直,则由椭圆的对称性得A(x1,y1),B(x1,-y1),
∵
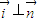 ,
,∴
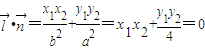 ,
,即y1=±2x1.
此时S=
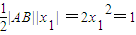 .
.当直线AB的斜率存在时,设直线AB为:kx-y+m=0,
设A(x1,kx1+m),B(x2,kx2+m),
则
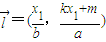 ,
,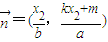 ,
,∵
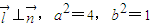 ,
,∴
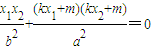 ,
,即(4+k2)x1x2+mk(x1+x2)+m2=0x1x2+mk(x1+x2)+m2=0,
由
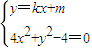 ,得(4+k2)x2+2kmx+m2-4=0,
,得(4+k2)x2+2kmx+m2-4=0,∴
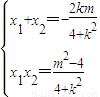 ,
,∴
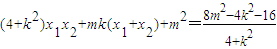 ,
,∵(4+k2)x1x2+mk(x1+x2)+m2=0,
∴8m2-4k2-16=0,即mk(x1+x2)+m2=0.
∵
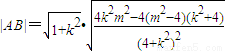
=
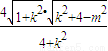
=
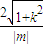 .
.原点O到kx-y+m=0的距离
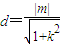 ,
,∴
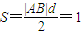 .
.综上所述,△AOB的面积是定值,等于1.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要灵活运用韦达定理、点到直线距离公式,注意合理地进行等价转化.

练习册系列答案
相关题目