题目内容
【题目】已知函数y=f(x)在R上的图象是连续不断的一条曲线,且图象关于原点对称,其导函数为f'(x),当x>0时,x2f'(x)>﹣2xf(x)成立,若x∈R,e2xf(ex)﹣a2x2f(ax)>0恒成立,则a的取值范围是_____.
【答案】0≤a<e
【解析】
构造g(x)=x2f(x),利用x2f'(x)>﹣2xf(x),可得g(x)在(0,+∞)上单调递增,转化e2xf(ex)﹣a2x2f(ax)>0,为g(ex)>g(ax),即可得ex>ax,分x=0,x>0,x<0三种情况讨论,参变分离即得解.
令g(x)=x2f(x),
因为x>0时,x2f'(x)>﹣2xf(x)
可知x>0时g'(x)=2xf(x)+x2f(x)>0,
g(x)在(0,+∞)上单调递增,
又因为函数y=f(x)在R上的图象是连续不断的一条曲线,且图象关于原点对称,
所以g(x)为R上单调递增的奇函数,
因为e2xf(ex)﹣a2x2f(ax)>0,所以g(ex)>g(ax),
即可得ex>ax,
当x=0时,1>0恒成立,
当x>0时,a![]() 恒成立,所以a
恒成立,所以a![]() ,
,
当x<0时,a![]() 恒成立,所以
恒成立,所以![]() ,
,
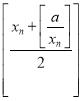
令h(x)![]() ,h'(x)
,h'(x)![]() ,
,
所以h(x)在(﹣∞,0),(0,1)上单调递减,在(1,+∞)上单调递增,
h(1)=e,
当x<0时,h(x)<0,
所以0≤a<e,

练习册系列答案
相关题目