题目内容
【题目】记[x]为不超过实数x的最大整数,例如,[2]=2,[1.5]=1,[-0.3]=-1.设a为正整数,数列{xn}满足x1=a,xn+1=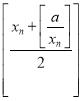 (n∈N*).现有下列命题:
(n∈N*).现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,xn>![]() -1;
-1;
④对某个正整数k,若xk+1≥xk,则xk=[![]() ].
].
其中的真命题有________.
【答案】①③④
【解析】①当![]() 时,
时, 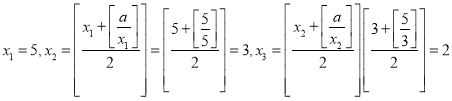 ,
,
该说法正确;
②当![]() 时,
时,
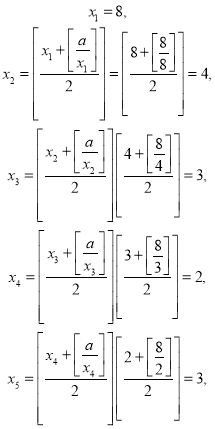
该数列是从第三项开始为![]() 的摆动数列,该说法错误;
的摆动数列,该说法错误;
③当![]() 时,
时, ![]() ,
,
则: ![]() 成立;
成立;
假设![]() 时,
时, ![]() ,
,
当![]() 时,
时, 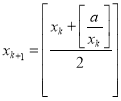 ,而:
,而:
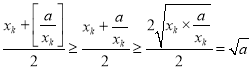 ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
故: 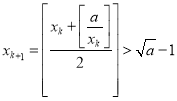 ,
,
对于任意的正整数n,当![]() 时,
时, ![]() ,该说法正确;
,该说法正确;
④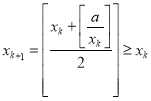 ,由①②的规律可得
,由①②的规律可得![]() 一定成立.
一定成立.
综上可得,真命题有①③④.

练习册系列答案
相关题目
