题目内容
(12分)已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)= +6x的图象关于y轴对称.
+6x的图象关于y轴对称.
(1)求m、n的值及函数y=f(x)的单调区间;(6分)
(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.(6分)
(1) f(x)的单调递减区间是(0,2).
(2)当0<a<1时,f(x)有极大值-2,无极小值;
当1<a<3时,f(x)有极小值-6,无极大值;
当a=1或a≥3时,f(x)无极值.
【解析】(Ⅰ)利用条件的到两个关于m、n的方程,求出m、n的值,再找函数y=f(x)的导函数大于0和小于0对应的区间即可.(Ⅱ)利用(Ⅰ)的结论,分情况讨论区间(a-1,a+1)和单调区间的位置关系再得结论.
(1)由函数f(x)的图象过点(-1,-6),得m-n=-3.①…
由f(x)=x3+mx2+nx-2,得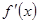 =3x2+2mx+n,………………2分
=3x2+2mx+n,………………2分
则g(x)=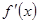 +6x=3x2+(2m+6)x+n.
+6x=3x2+(2m+6)x+n.
而g(x)的图象关于y轴对称,所以-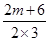 =0,解得 m=-3.
=0,解得 m=-3.
代入①得n=0.
于是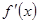 =3x2-6x=3x(x-2).………………………4分
=3x2-6x=3x(x-2).………………………4分
由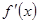 >0得x>2或x<0,
>0得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);………………………5分
由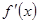 <0,得0<x<2,
<0,得0<x<2,
故f(x)的单调递减区间是(0,2).………………………6分
(2)由(1)得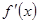 =3x(x-2),令
=3x(x-2),令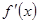 =0得x=0或x=2. ………………7分
=0得x=0或x=2. ………………7分
当x变化时,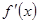 ,f(x)的变化情况如下表:
,f(x)的变化情况如下表:
|
x |
(-∞,0) |
0 |
(0,2) |
2 |
(2,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
f(x) |
增函数? |
极大值 |
减函数 |
极小值 |
增函数? |
…………………………………9分
由此可得:当0<a<1时,f(x)在(a-1,a+1)内有极大值f(0)=-2,无极小值;
当a=1时,f(x)在 (a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得,当0<a<1时,f(x)有极大值-2,无极小值;
当1<a<3时,f(x)有极小值-6,无极大值;
当a=1或a≥3时,f(x)无极值.………………………………12分

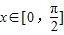 ,求f(x)的最大值,最小值.
,求f(x)的最大值,最小值. (x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为
(x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为 。
。 }的通项公式为
}的通项公式为 )(m∈N
)(m∈N ,n=1,2,3,…,m),求数列{
,n=1,2,3,…,m),求数列{ ; (5分)
; (5分) <
< 横成立,求实数a的取值范围。(3分)
横成立,求实数a的取值范围。(3分)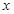 )=
)= ,当
,当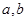 的值及函数f(
的值及函数f( f(
f( ,问
,问