题目内容
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数 与时刻
与时刻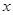 (时)的关系为
(时)的关系为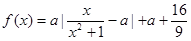 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且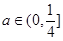 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作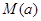 .
.
(1)令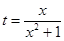 ,
, ,求
,求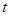 的取值范围;
的取值范围;
(2)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
(1)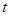 的取值范围是
的取值范围是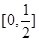 ;(2)当
;(2)当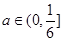 时,污染指数不超标;当
时,污染指数不超标;当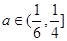 时,污染指数超标.
时,污染指数超标.
解析试题分析:(1)从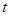 的表达式可知,可以考虑利用基本不等式求
的表达式可知,可以考虑利用基本不等式求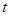 的取值范围,首先讨论当当
的取值范围,首先讨论当当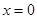 时,
时,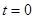 ,而当
,而当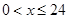 时:
时: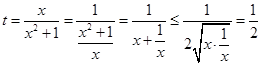 ,
,
当且仅当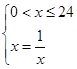 ,即
,即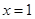 时取等号,而显然
时取等号,而显然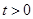 ,因此
,因此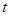 的取值范围是
的取值范围是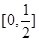 ;(2)根据条件结合(1)分析可知,可将污染指数转化为与
;(2)根据条件结合(1)分析可知,可将污染指数转化为与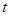 有关的函数
有关的函数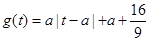 ,利用(1)中求得的
,利用(1)中求得的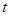 的取值范围,可知
的取值范围,可知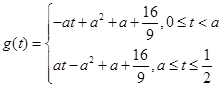 ,显然
,显然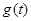 在
在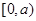 上单调递减,在
上单调递减,在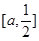 上单调递增,∴
上单调递增,∴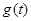 的最大值只可能在
的最大值只可能在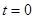 或
或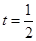 时取到,通过比较可知
时取到,通过比较可知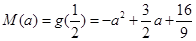 ,从而若市中心的污染指数未超标,则等价于
,从而若市中心的污染指数未超标,则等价于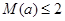 ,解关于
,解关于 的不等式组
的不等式组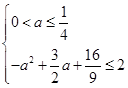 ,从而可以得到相应结论:当
,从而可以得到相应结论:当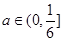 时,污染指数不超标;当
时,污染指数不超标;当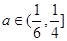 时,污染指数超标.
时,污染指数超标.
试题解析:(1)当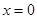 时:
时: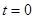 , 1分
, 1分
当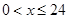 时:
时: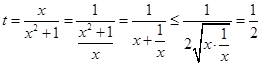 , 4分
, 4分
当且仅当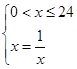 ,即
,即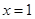 时取等号, 5分 而显然
时取等号, 5分 而显然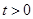 ,
,
综上所述,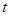 的取值范围是
的取值范围是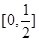 ; 6分
; 6分
(2)记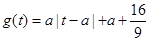 ,
,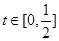 ,则
,则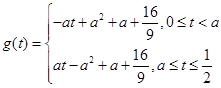 , 8分
, 8分
显然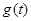 在
在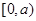 上单调递减,在
上单调递减,在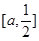 上单调递增,∴
上单调递增,∴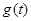 的最大值只可能在
的最大值只可能在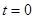 或
或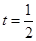 时取到,
时取到,
而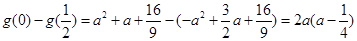 ,∵
,∵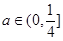 ,∴
,∴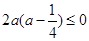 ,
,
∴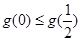 ,∴
,∴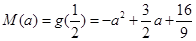 , 11分
, 11分
由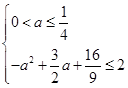 得
得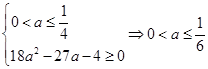 , 13分
, 13分
故当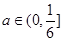 时,污染指数不超标;当
时,污染指数不超标;当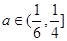 时,污染指数超标. 14分
时,污染指数超标. 14分
考点:1.基本不等式求函数值域;2.分段函数的综合运用.

练习册系列答案
相关题目
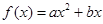 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为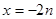 ,
,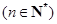 .
.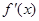 是
是 的导函数,且
的导函数,且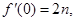
 );
); 满足
满足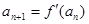 ,且
,且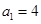 ,求数列
,求数列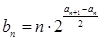 ,
,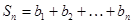 ,是否存在自然数
,是否存在自然数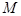 ,使得当
,使得当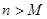 时
时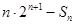
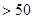 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的 (
( ).
). 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;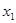 ,
,
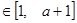 ,总有
,总有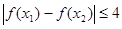 ,求实数
,求实数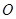 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 ,圆心角为
,圆心角为 (弧度).
(弧度). ,求
,求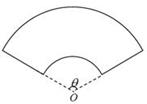
 定义域为
定义域为 .
. ,求实数
,求实数 的取值范围;
的取值范围; 在
在 上恒成立,求实数
上恒成立,求实数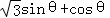 ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.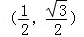 ,求f(θ)的值;
,求f(θ)的值;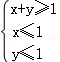 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
 和
和 是方程
是方程 的两个实根,不等式
的两个实根,不等式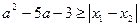 对任意实数
对任意实数 恒成立,则
恒成立,则 的取值范围是
的取值范围是