题目内容
已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,求a的值.
a=2,或a=-1
解析试题分析:因为函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,通过配方可知函数的对称轴为x=a,且知该二次函数的开口向下,按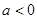 、
、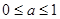 、
、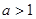 分类讨论,结合图象就可用a将函数在[0,1]的最大值表示出来,再令其等于2就可解得a值.
分类讨论,结合图象就可用a将函数在[0,1]的最大值表示出来,再令其等于2就可解得a值.
试题解析:由f(x)=-x2+2ax+1-a=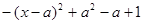 知其对称轴为:
知其对称轴为: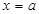 ,又因为x∈[0,1];
,又因为x∈[0,1];
(1)当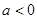 时,函数
时,函数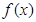 在[0,1]上是减函数,所以
在[0,1]上是减函数,所以 ;
;
(2)当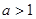 时,函数
时,函数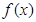 在[0,1]上是增函数,所以
在[0,1]上是增函数,所以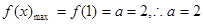 ;
;
(3)当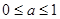 时,函数
时,函数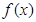 在[0,1]上的最大值为
在[0,1]上的最大值为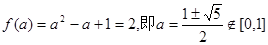 故舍去.
故舍去.
综上可知:a=2,或a=-1
考点:1.二次函数在闭区间上的最值;2.分类讨论.

练习册系列答案
相关题目
 与时刻
与时刻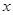 (时)的关系为
(时)的关系为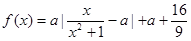 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且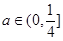 ,用每天
,用每天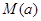 .
.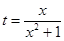 ,
,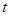 的取值范围;
的取值范围; (x∈R,且x≠2).
(x∈R,且x≠2). 的单调区间;
的单调区间;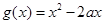 与函数
与函数 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值;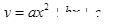 的图象与
的图象与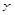 轴交于
轴交于 的充要条件为
的充要条件为 .
. 是边长为
是边长为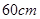 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
. 最大,试问
最大,试问 应取何值?
应取何值? 最大,试问
最大,试问

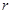 米,高为
米,高为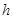 米,体积为
米,体积为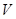 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为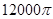 元(
元(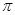 为圆周率).
为圆周率).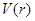 ,并求该函数的定义域;
,并求该函数的定义域;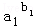
 …
…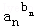 ≤1;
≤1; ≤
≤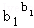
 …
…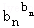 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2.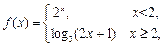 若
若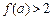 , 则a的取值范围是 .
, 则a的取值范围是 .