题目内容
已知函数 (
( ).
).
(1)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(2)若对任意的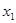 ,
,
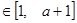 ,总有
,总有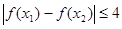 ,求实数
,求实数 的取值范围.
的取值范围.
(1)  ; (2)
; (2) 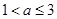 .
.
解析试题分析:(1)首先用配方法求出二次函数 的对称轴为
的对称轴为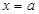 ,由于
,由于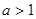 ,知函数
,知函数 在已知区间
在已知区间 是为减函数,要使函数定义域和值域均为
是为减函数,要使函数定义域和值域均为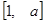 ,必须且只需
,必须且只需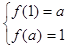 ,从而得到关于a的方程组,解此方程组得实数
,从而得到关于a的方程组,解此方程组得实数 的值;(2)因为对任意的
的值;(2)因为对任意的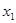 ,
,
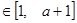 ,总有
,总有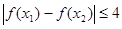 ,等价于:
,等价于: ,所以问题转化为求函数
,所以问题转化为求函数 在
在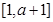 的最大值和最小值;由于二次函数
的最大值和最小值;由于二次函数 的开口向上,且对称轴为
的开口向上,且对称轴为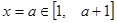 ,所以其最小值一定是
,所以其最小值一定是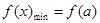 ,而最大值就是两个端点值所对函数值中的较大者,由二次函数的性质可知:等价于比较两个区间的端点谁离对称轴远些;由此只需按
,而最大值就是两个端点值所对函数值中的较大者,由二次函数的性质可知:等价于比较两个区间的端点谁离对称轴远些;由此只需按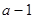 与1的大小进行分类讨论,即可用a的代数式表示出函数
与1的大小进行分类讨论,即可用a的代数式表示出函数 在
在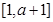 的最大值和最小值,然后代入
的最大值和最小值,然后代入 就可求得a的取值范围.
就可求得a的取值范围.
试题解析:(1)∵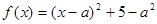 (
(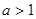 ),
),
∴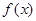 在
在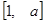 上是减函数,又定义域和值域均为
上是减函数,又定义域和值域均为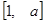 ,∴
,∴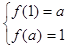 ,
,
即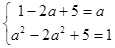 , 解得
, 解得  .
.
(2)若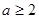 ,又
,又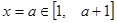 ,且
,且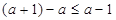 ,
,
∴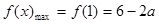 ,
,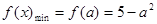 .
.
∵对任意的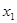 ,
,
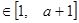 ,总有
,总有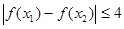 ,
,
∴ , 即
, 即 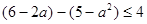 ,解得
,解得 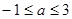 ,
,
又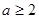 , ∴
, ∴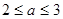 .
.
若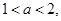
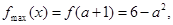
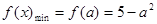 ,
, 显然成立,
显然成立,
综上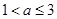 .
.
考点:1.二次函数的单调性与最值;2.分类讨论.

练习册系列答案
相关题目

 =
=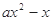 (
( ,
,
 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; 与
与 的图像有两个不同的交点
的图像有两个不同的交点 ,求
,求 的取值范围。
的取值范围。 和
和 (
( 是函数
是函数 的切线以
的切线以 为切点,求证
为切点,求证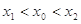 .
. 与时刻
与时刻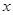 (时)的关系为
(时)的关系为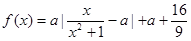 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且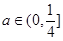 ,用每天
,用每天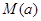 .
.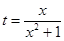 ,
,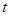 的取值范围;
的取值范围; 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元. ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值; +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称. ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围. ,若
,若 ,则
,则 .
. ,若
,若 ,则a的取值范围是 .
,则a的取值范围是 .