题目内容
若函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,则实数a的取值范围是_________.解析:本题考查复合函数单调性的判定方法,要注意判断函数的单调性必须在函数的定义域内进行.
∵函数f(x)在区间[2,+∞)上单调递增,
∴-![]() ≤2,且x=2时,x2+ax-a-1>0,即
≤2,且x=2时,x2+ax-a-1>0,即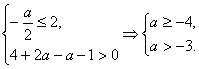
∴a>-3,即实数a的取值范围是(-3,+∞).
答案:(-3,+∞).

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目