题目内容
下列命题:
(1)若函数f(x)=lg(x+
)为奇函数,则a=1;
(2)函数f(x)=|1+sinx+cosx|的周期T=2π;
(3)方程lgx=sinx有且只有三个实数根;
(4)对于函数f(x)=
,若0<x1<x2,则f(
)<
.
以上命题为真命题的是
(1)若函数f(x)=lg(x+
| x2+a |
(2)函数f(x)=|1+sinx+cosx|的周期T=2π;
(3)方程lgx=sinx有且只有三个实数根;
(4)对于函数f(x)=
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
以上命题为真命题的是
(1)(2)(3)
(1)(2)(3)
.(将所有真命题的序号填在题中的横线上)分析:(1)已知函数奇偶性,求参数的值,常用特殊值验证,代入x=0或1即得;
(2)先对函数化简整理得到f(x)=|1+
sin(x+
)|,再有函数图象的平移、对称变换得到f(x)的图象,即得f(x)的周期;
(3)在同一坐标系中,作出y=lgx与y=sinx的图象,看交点个数;(数形结合)
(4)(数形结合)作出函数f(x)=
的图象,即可判定两值的大小关系.
(2)先对函数化简整理得到f(x)=|1+
| 2 |
| π |
| 4 |
(3)在同一坐标系中,作出y=lgx与y=sinx的图象,看交点个数;(数形结合)
(4)(数形结合)作出函数f(x)=
| x |
解答:解:(1)∵函数f(x)=lg(x+
)为奇函数,
∴f(0)=0,即f(0)=lg(0+
)=lg
=0,
∴
=1,即a=1;
(2)∵f(x)=|1+sinx+cosx|=|1+
sin(x+
)|,
又由y=
sin(x+
)的周期是2π,将其函数图象上移一个单位后得到y=
sin(x+
)+1的图象,
然后再将X轴下方的图象沿X轴旋转180°,得到f(x)=1+
sin(x+
)|的图象,
∴函数f(x)=|1+sinx+cosx|的周期T=2π;
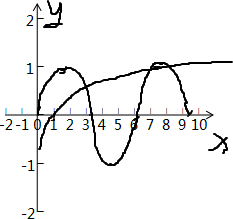
(3)作出y=lgx与y=sinx的图象,由于y=lgx在(0,∞)上为增函数且l,g10=1,lg1=0,
故在区间(0,π)内y=lgx与y=sinx有一个交点,在(π,2π)内无交点,在(2π,3π)内有三个交点,
∴方程lgx=sinx有且只有三个实数根;
(4)∵函数f(x)=
是单调递增的凸函数,∴在0<x1<x2,则f(
)>
,
∴若0<x1<x2,则f(
)<
是错误的;
故答案为(1)(2)(3).
| x2+a |
∴f(0)=0,即f(0)=lg(0+
| 0+a |
| a |
∴
| a |
(2)∵f(x)=|1+sinx+cosx|=|1+
| 2 |
| π |
| 4 |
又由y=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
然后再将X轴下方的图象沿X轴旋转180°,得到f(x)=1+
| 2 |
| π |
| 4 |
∴函数f(x)=|1+sinx+cosx|的周期T=2π;
(3)作出y=lgx与y=sinx的图象,由于y=lgx在(0,∞)上为增函数且l,g10=1,lg1=0,
故在区间(0,π)内y=lgx与y=sinx有一个交点,在(π,2π)内无交点,在(2π,3π)内有三个交点,
∴方程lgx=sinx有且只有三个实数根;

(4)∵函数f(x)=
| x |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
∴若0<x1<x2,则f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故答案为(1)(2)(3).
点评:本题考查的知识点是命题的真假判定,同时考查了函数的一些性质,注意数形结合的方法.

练习册系列答案
相关题目
 (0<x<1)的最大函数值为
(0<x<1)的最大函数值为 ;
; ≥
≥ .
.