题目内容
若函数f(x)=lg(x2+ax-a-1)在区间［2,+∞)上单调递增,则实数a的取值范围是 .
(-3,+∞)
解析:∵函数f(x)在区间［2,+∞）上单调递增,
∴-
≤2,且x=2时,x2+ax-a-1＞0,即
∴
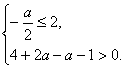
∴a＞-3,即实数a的取值范围是(-3,+∞).
练习册系列答案
相关题目
题目内容
若函数f(x)=lg(x2+ax-a-1)在区间［2,+∞)上单调递增,则实数a的取值范围是 .
(-3,+∞)
解析:∵函数f(x)在区间［2,+∞）上单调递增,
∴-≤2,且x=2时,x2+ax-a-1＞0,即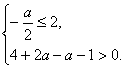
∴
∴a＞-3,即实数a的取值范围是(-3,+∞).