题目内容
点A、B分别是椭圆 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值.
的最小值.

 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于
 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值.
的最小值.
(1)由已知可得点A(-6,0),F(0,4)
设点P( ,
, ),则
),则 ={
={ +6,
+6,  },
}, ={
={ -4,
-4,  },由已知可得
},由已知可得
 则2
则2 +9
+9 -18=0,
-18=0, =
= 或
或 =-6.
=-6.
由于 >0,只能
>0,只能 =
= ,于是
,于是 =
= . ∴点P的坐标是(
. ∴点P的坐标是( ,
, )
)
(2) 直线AP的方程是 -
-
 +6="0. " 设点M(
+6="0. " 设点M( ,0),则M到直线AP的距离是
,0),则M到直线AP的距离是 . 于是
. 于是 =
= ,又-6≤
,又-6≤ ≤6,解得
≤6,解得 =2.
=2.
椭圆上的点( ,
, )到点M的距离
)到点M的距离 有
有
 ,
,
由于-6≤ ≤6, ∴当
≤6, ∴当 =
= 时,d取得最小值
时,d取得最小值
设点P(
 ,
, ),则
),则 ={
={ +6,
+6,  },
}, ={
={ -4,
-4,  },由已知可得
},由已知可得 则2
则2 +9
+9 -18=0,
-18=0, =
= 或
或 =-6.
=-6.由于
 >0,只能
>0,只能 =
= ,于是
,于是 =
= . ∴点P的坐标是(
. ∴点P的坐标是( ,
, )
)(2) 直线AP的方程是
 -
-
 +6="0. " 设点M(
+6="0. " 设点M( ,0),则M到直线AP的距离是
,0),则M到直线AP的距离是 . 于是
. 于是 =
= ,又-6≤
,又-6≤ ≤6,解得
≤6,解得 =2.
=2.椭圆上的点(
 ,
, )到点M的距离
)到点M的距离 有
有 ,
,由于-6≤
 ≤6, ∴当
≤6, ∴当 =
= 时,d取得最小值
时,d取得最小值
设椭圆上动点坐标为(x,y),用该点的横坐标将距离d表示出来,利用求函数最值的方法求d的最小值. 点评:解决有关最值问题时,首先要恰当地引入变量(如点的坐标、角、斜率等),建立目标函数,然后利用函数的有关知识和方法求解.

练习册系列答案
相关题目
 ,
, )
) )
) )
) )
) 上的点到直线
上的点到直线 的距离的最小值和最大值.
的距离的最小值和最大值.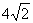 -4,求此椭圆方程、离心率、准线方程及准线间的距离.
-4,求此椭圆方程、离心率、准线方程及准线间的距离. 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过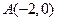 、
、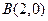 、
、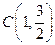 三点. (1)求椭圆
三点. (1)求椭圆 、
、 的任意一点,
的任意一点, ,当
,当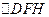 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线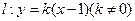 与椭圆
与椭圆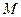 、
、 两点,证明直线
两点,证明直线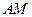 与直线
与直线 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程. ,求实数λ的取值范围.
,求实数λ的取值范围. 的倾斜角为 .
的倾斜角为 . 的倾斜角和斜率分别是( )
的倾斜角和斜率分别是( ) ,不存在
,不存在

 ,不存在
,不存在 上的一点P作圆
上的一点P作圆 的两条切线
的两条切线 为切点,当直线
为切点,当直线 关于直线
关于直线 对称时,
对称时, .
.