题目内容
一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元.
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
答案见解析
解:(1)设该厂的月获利为y,依题意得y=(160-2x)x-(500+30x)=-2x2+130x-500
由y≥1300知-2x2+130x-500≥1300
∴x2-65x+900≤0,∴(x-20)(x-45)≤0,解得20≤x≤45
∴当月产量在20~45件之间时,月获利不少于1300元.
(2)由(1)知y=-2x2+130x-500=-2(x-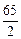 )2+1612.5
)2+1612.5
∵x为正整数,∴x=32或33时,y取得最大值为1612元,
∴当月产量为32件或33件时,可获得最大利润1612元.
由y≥1300知-2x2+130x-500≥1300
∴x2-65x+900≤0,∴(x-20)(x-45)≤0,解得20≤x≤45
∴当月产量在20~45件之间时,月获利不少于1300元.
(2)由(1)知y=-2x2+130x-500=-2(x-
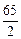 )2+1612.5
)2+1612.5∵x为正整数,∴x=32或33时,y取得最大值为1612元,
∴当月产量为32件或33件时,可获得最大利润1612元.

练习册系列答案
相关题目
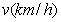 的平方成正比,比例系数为2, 固定部分为3000元.
的平方成正比,比例系数为2, 固定部分为3000元.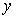 (元)表示为速度
(元)表示为速度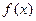 为定义在R上的偶函数,当
为定义在R上的偶函数,当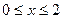 时,
时,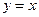 ;当
;当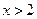 时,
时,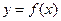 的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分.
的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分.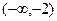 上的解析式;
上的解析式;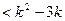 对
对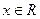 恒成立,求
恒成立,求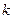 的取值范围。
的取值范围。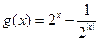 .
.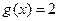 ,求
,求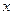 的值;
的值;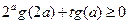 对于
对于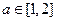 恒成立,求实数
恒成立,求实数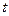 的取值范围.
的取值范围.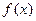 是二次函数,若
是二次函数,若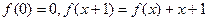 ,则
,则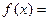
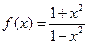 ,则
,则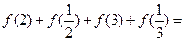 。
。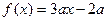 +1在[—1,1]上存在一个零点,则a的取值范围为 。
+1在[—1,1]上存在一个零点,则a的取值范围为 。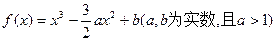 在区间
在区间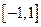 上最大值为1,最小值为
上最大值为1,最小值为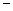 2.(1)求
2.(1)求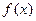 的解析式;(2)若函数
的解析式;(2)若函数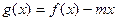 在区间
在区间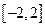 上为减函数,求实数m的取值范围.
上为减函数,求实数m的取值范围.