题目内容
.内有任意三点都不共线的2009个点,加上三个顶点,共2012个点,把这2012个点连线形成互不重叠的小三角形,则一共可以形成的小三角形的个数为( )
| A.4010 | B.4013 | C.4017 | D.4019 |
D
专题:计算题.
分析:根据题意,分析易得:△ABC中有1个点时,△ABC中有2个点时,△ABC中有3个点时,可以形成小三角形的个数,由归纳推理的方法可得当三角形中有n个点时,可以形成三角形的个数,将n=2009代入可得答案.
解答:解:△ABC中有1个点时,可以形成小三角形的个数为2×1+1=3个,
△ABC中有2个点时,可以形成小三角形的个数为2×2+1=5个,
△ABC中有3个点时,可以形成小三角形的个数为2×3+1=7个,
…,
分析可得,当△ABC的内部每增加一个点,可以形成小三角形的数目增加2个,
则三角形中有n个点时,三角形的个数为(2n+1)个;
当△ABC内有任意三点不共线的2009个点时,应有点2×2009+1=4019;
故选D.
点评:本题考查图形的变化规律,关键是分析得到三角形的个数与三角形内点的个数的变化规律.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
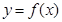 在点
在点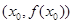 处的 切线方程为
处的 切线方程为 ,则( )
,则( )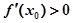
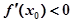
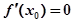
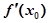 不存在
不存在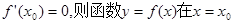 取得极值;
取得极值;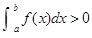 ,则f(x)>0在
,则f(x)>0在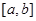 上恒成立;
上恒成立;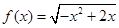 ,则
,则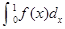 的值为
的值为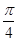 ;
;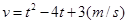 运动,从时刻
运动,从时刻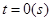 到
到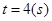 时质点运动的路程为
时质点运动的路程为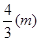 。
。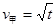 ,
,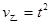 (如右上图);当甲,乙行走的速度相同(不为零)时刻:
(如右上图);当甲,乙行走的速度相同(不为零)时刻: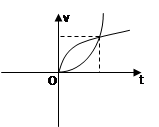
 a
a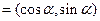 ,b
,b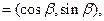 且a,b满足|ka+b |=
且a,b满足|ka+b |=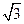 |a-kb|
|a-kb|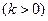 ,
,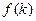 ;
; 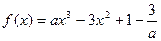
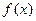 在
在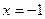 时取得极值,求实数
时取得极值,求实数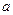 的值;
的值;
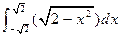 = 。
= 。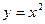 上一点P处的切线与直线
上一点P处的切线与直线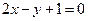 平行,则点P的坐标为( )
平行,则点P的坐标为( )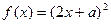 ,且
,且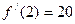 ,则
,则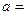 __________________.
__________________.