题目内容
函数y=(
)|x|的图象有什么特征?你能根据图象指出其值域和单调区间吗?
| 1 | 2 |
分析:根据绝对值的几何意义及指数函数的图象,可得函数的图象及特征,利用图象可得函数值域和单调区间.
解答:解:因为|x|=
,所以当x≥0时,函数为y=(
)x;当x<0时,函数为y=(
)-x=2x,
其图象由y=(
)x(x≥0)和y=2x(x<0)的图象合并而成.
而y=(
)x(x≥0)和y=2x(x<0)的图象关于y轴对称,所以原函数图象关于y轴对称.
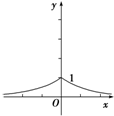
由图象可知值域是(0,1],递增区间是(-∞,0],递减区间是[0,+∞).
|
| 1 |
| 2 |
| 1 |
| 2 |
其图象由y=(
| 1 |
| 2 |
而y=(
| 1 |
| 2 |

由图象可知值域是(0,1],递增区间是(-∞,0],递减区间是[0,+∞).
点评:本题考查函数的图象的画法,考查利用函数图象解决问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若由函数y=(
)x的图象平移得到函数y=2-x+1+2的图象,则平移过程可以是( )
| 1 |
| 2 |
| A、先向左平移1个单位,再向上平移2个单位 |
| B、先向左平移1个单位,再向下平移2个单位 |
| C、先向右平移1个单位,再向上平移2个单位 |
| D、先向右平移1个单位,再向下平移2个单位 |