题目内容
函数y=(
)x在[1,2]上的值域为( )
| 1 |
| 2 |
分析:利用指数函数的单调性,求出函数在[1,2]上的最大、最小值,即可得到函数在[1,2]上的值域.
解答:解:∵
∈(0,1),
∴指数函数y=(
)x在[1,2]上为减函数,
可得函数的最大值为f(1)=
,最小值为f(2)=
.
因此,函数y=(
)x在[1,2]上的值域为[
,
].
故选:D
| 1 |
| 2 |
∴指数函数y=(
| 1 |
| 2 |
可得函数的最大值为f(1)=
| 1 |
| 2 |
| 1 |
| 4 |
因此,函数y=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
故选:D
点评:本题给出指数函数,求函数在给定区间上的值域.着重考查了指数函数的单调性和函数值域的求法等知识,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
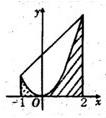 如图,设T是直线x=-1,x=2与函数y=x2的图象在x轴上方围成的直角梯形区域,S是T内函数y=x2图象下方的点构成的区域(图中阴影部分).向T中随机投一点,则该点落入S中的概率为( )
如图,设T是直线x=-1,x=2与函数y=x2的图象在x轴上方围成的直角梯形区域,S是T内函数y=x2图象下方的点构成的区域(图中阴影部分).向T中随机投一点,则该点落入S中的概率为( )