题目内容
已知函数f(x)是定义域为[-1,0)∪(0,1],其图象上的任意一点P(x,y)满足x2+y2=1,则下列命题正确的是
①函数y=f(x)一定是偶函数;
②函数y=f(x)可能既不是奇函数,也不是偶函数;
③函数y=f(x)可能是奇函数;
④函数y=f(x)若是偶函数,则值域是[-1,0)或(0,1];
⑤函数y=f(x)的值域是(-1,1),则函数f(x)一定是奇函数.
②③⑤
②③⑤
.(写出所有正确命题的编号)①函数y=f(x)一定是偶函数;
②函数y=f(x)可能既不是奇函数,也不是偶函数;
③函数y=f(x)可能是奇函数;
④函数y=f(x)若是偶函数,则值域是[-1,0)或(0,1];
⑤函数y=f(x)的值域是(-1,1),则函数f(x)一定是奇函数.
分析:根据函数奇偶性的定义和函数的定义分别进行判断即可.
解答: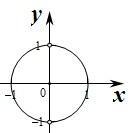 解:∵P(x,y)满足x2+y2=1,
解:∵P(x,y)满足x2+y2=1,
∴P位于单位圆上.
①当函数y=f(x)对应的图象在第一象限和第三象限时,函数为奇函数,∴①错误.
②函数y=f(x)可能既不是奇函数,也不是偶函数,正确.
③当函数y=f(x)对应的图象在第一象限和第三象限时,函数为奇函数,∴③正确;
④函数y=f(x)若是偶函数,则值域是(-1,0]或[0,1),∴④错误.
⑤函数y=f(x)的值域是(-1,1),则根据函数的定义可知,此时函数对应的图象为一,三象限或二,四象限的部分,∴根据图象的对称性可知,函数f(x)一定是奇函数.∴⑤正确.
故答案为:②③⑤.
 解:∵P(x,y)满足x2+y2=1,
解:∵P(x,y)满足x2+y2=1,∴P位于单位圆上.
①当函数y=f(x)对应的图象在第一象限和第三象限时,函数为奇函数,∴①错误.
②函数y=f(x)可能既不是奇函数,也不是偶函数,正确.
③当函数y=f(x)对应的图象在第一象限和第三象限时,函数为奇函数,∴③正确;
④函数y=f(x)若是偶函数,则值域是(-1,0]或[0,1),∴④错误.
⑤函数y=f(x)的值域是(-1,1),则根据函数的定义可知,此时函数对应的图象为一,三象限或二,四象限的部分,∴根据图象的对称性可知,函数f(x)一定是奇函数.∴⑤正确.
故答案为:②③⑤.
点评:本题主要考查函数奇偶性的定义和应用,利用函数的定义和单位圆,结合数形结合是解决本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+