题目内容
三棱锥A-BCD每个面都是正三角形，点p是平面ABC内任意一点，若p到点A的距离等于p到平面BCD的距离，则p的轨迹是 ．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：将点P到平面ABC距离与到点A的距离相等转化成在面ABC中点P到A的距离与到定直线BC的距离比是一个常数，依据圆锥曲线的第二定义判断出其轨迹的形状．
解答：
解：设二面角A-BC-D的平面角为θ，点P到平面BCD的距离为|PH|，点P到定直线CB的距离为d，则|PH|=dsinθ
∵点P到平面BCD的距离与点P到点A的距离相等
∴dsinθ=|PA|
∴
=sinθ＜1
即在平面ABC中，点P到定点A的距离与定直线BC的距离之比是一个小于1的常数sinθ，
由椭圆定义知P点轨迹为椭圆在面ABC内的一部分．
故答案为：椭圆在面ABC内的一部分．
∵点P到平面BCD的距离与点P到点A的距离相等
∴dsinθ=|PA|
∴
| |PA| |
| d |
即在平面ABC中，点P到定点A的距离与定直线BC的距离之比是一个小于1的常数sinθ，
由椭圆定义知P点轨迹为椭圆在面ABC内的一部分．
故答案为：椭圆在面ABC内的一部分．
点评：本题主要考查立体几何中的轨迹问题，解题的关键是将点P到平面ABC距离与到点A的距离相等转化成在面ABC中点P到A的距离与到定直线BC的距离比是一个常数．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
命题“若x2＜1，则-1＜x＜1”的逆否命题是（ ）
| A、若x2≥1，则x≥1且x≤-1 |
| B、若-1＜x＜1，则x2＜1 |
| C、若x＞1或x＜-1，则x2＞1 |
| D、若x≥1或x≤-1，则x2≥1 |
有四个数a1，a2，a3，a4，前三个数成等比，积为64；后三个数成等差，和为6；则a1=（ ）
| A、9 | B、8 | C、16 | D、4 |
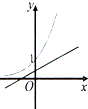
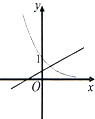
如图，设A为半径为1圆周上一定点，在圆周上等可能的任取一点B，则弦长|AB|超过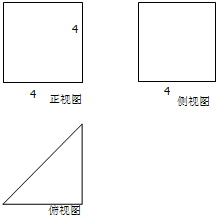
一个几何体的三视图如图所示，则这个几何体的表面积等于