题目内容
2.在△ABC中,角A、B、C的对边分别为a、b、c,且acosC+$\sqrt{3}$asinC-b-c=0①求角A的大小;
②若a=2,△ABC的面积为$\sqrt{3}$,求b、c的值.
分析 (1)由正弦定理及两角和的正弦公式可得sinAcosC+$\sqrt{3}$sinAsinC=sinB+sinC=sin(A+C)+sinC=sinAcosC+sinCcosA+sinC,整理可求A.
(2)由(1)所求A及S=$\frac{1}{2}$bcsinA可求bc,然后由余弦定理,a2=b2+c2-2bccosA=(b+c)2-2bc-2bccosA可求b+c,进而可求b,c.
解答 解:(1)∵acosC+$\sqrt{3}$asinC-b-c=0,
∴sinAcosC+$\sqrt{3}$sinAsinC-sinB-sinC=0,
∴sinAcosC+$\sqrt{3}$sinAsinC=sinB+sinC=sin(A+C)+sinC=sinAcosC+sinCcosA+sinC,
∵sinC≠0,
∴$\sqrt{3}$sinA-cosA=1,
∴sin(A-30°)=$\frac{1}{2}$,
∴A-30°=30°,
∴A=60°,
(2)由S=$\frac{1}{2}$bcsinA=$\sqrt{3}$?bc=4,
由余弦定理可得,a2=b2+c2-2bccosA=(b+c)2-2bc-2bccosA,
即4=(b+c)2-3bc=(b+c)2-12,
∴b+c=4,
解得:b=c=2.
点评 本题综合考查了三角公式中的正弦定理、余弦定理、三角形的面积公式的综合应用,诱导公式与辅助角公式在三角函数化简中的应用是求解的基础,解题的关键是熟练掌握基本公式.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
6.把函数y=sinx图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变)后,再将图象向左平移$\frac{π}{4}$个单位,那么所得图象的一条对称轴方程为( )
| A. | $x=-\frac{π}{2}$ | B. | $x=-\frac{π}{4}$ | C. | $x=\frac{π}{8}$ | D. | $x=\frac{π}{4}$ |
7.某校有一个班级,设变量x是该班同学的姓名,变量y是该班同学的学号,变量z是该班同学的身高,变量w是该班同学某一门课程的考试成绩,则下列选项中一定正确的是(( )
| A. | y是x的函数 | B. | z是y的函数 | C. | w是z的函数 | D. | w是x的函数 |
7.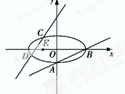 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )| A. | $\frac{7}{6}$ | B. | -$\frac{7}{6}$ | C. | 3 | D. | 6 |
12.已知命题p:?x∈R,x-2>lgx,命题q:?x>-1,ex>ln(x+1),则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
 已知二次函数f(x)=ax2+bx+2的导函数的图象如图所示:
已知二次函数f(x)=ax2+bx+2的导函数的图象如图所示:


