题目内容
若平面直角坐标系中两点M，N满足条件：
①M，N分别在函数f（x），g（x）的图象上；
②M，N关于（1，O）对称，则称点对（M，N）是一个“相望点对”（说明：（M，N）和（N，M）是同一个“相望点对”）．
函数y=
与y=2sinπx（-2≤x≤4）的图象中“相望点对”的个数是（ ）
①M，N分别在函数f（x），g（x）的图象上；
②M，N关于（1，O）对称，则称点对（M，N）是一个“相望点对”（说明：（M，N）和（N，M）是同一个“相望点对”）．
函数y=
| 1 |
| 1-x |
| A．2 | B．4 | C．6 | D．8 |
由题意，函数y=
与y=2sinπx（-2≤x≤4）的图象均关于（1，0）对称，
当-2≤x≤1时，函数y=
与y=2sinπx的图象在（-2，-1），（0，1）上分别有2个交点
∴根据“相望点对”的定义，可得函数y=
与y=2sinπx（-2≤x≤4）的图象中“相望点对”的个数是4
故选B．
| 1 |
| 1-x |
当-2≤x≤1时，函数y=
| 1 |
| 1-x |
∴根据“相望点对”的定义，可得函数y=
| 1 |
| 1-x |
故选B．
练习册系列答案
相关题目
设A1，A2，A3，A4是平面直角坐标系中两两不同的四点，若
=λ
（λ∈R），
=μ
（μ∈R），且
+
=2，则称A3，A4调和分割A1，A2，已知点C（c，0），D（d，O）（c，d∈R）调和分割点A（0，0），B（1，0），则下面说法正确的是（ ）
| A1A3 |
| A1A2 |
| A1A4 |
| A1A2 |
| 1 |
| λ |
| 1 |
| μ |
| A、C可能是线段AB的中点 |
| B、D可能是线段AB的中点 |
| C、C，D可能同时在线段AB上 |
| D、C，D不可能同时在线段AB的延长线上 |
，
，
，
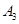是平面直角坐标系中两两不同的四点，若
(λ∈R)，
(μ∈R)，且
,则称
，
，
，
是平面直角坐标系中两两不同的四点，若
，
，且
,则称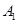
，
，
，
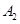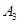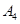是平面直角坐标系中两两不同的四点，若
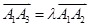(λ∈R)， 
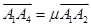(μ∈R)，且
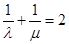,则称
，
，
，
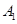是平面直角坐标系中两两不同的四点，若
（λ∈R），
（μ∈R），且,
，则称