题目内容
4.已知函数f(x)=log4(4x+1)-(k-1)x(x∈R)为偶函数.(1)求常数k的值,并指出当x取何值时函数f(x)的值最小?并求出f(x)的最小值;
(2)设g(x)=log4(a•2x-$\frac{4}{3}$a)(a≠0),且函数f(x)与g(x)的图象有公共点,求实数a的取值范围
(3)指出实数a不同取值时,(2)中函数图象交点的个数.
分析 (1)由f(x)是定义域R上的偶函数,得f(-x)=f(x),取特殊值x=1,求出k的值;
利用偶函数的图象与性质,得出x=0时f(x)的值最小,求出最小值f(0);
(2)利用g(x)=f(x),讨论方程的实数解与函数零点的关系,求出两函数图象有公共点时a的取值范围;
(3)由(2)知,函数f(x)与g(x)的图象有1个或2个交点时,对应a的取值范围.
解答 解:(1)∵函数f(x)=log4(4x+1)-(k-1)x为定义域R上的偶函数,
∴f(-x)=f(x),
即log4(4-x+1)-(k-1)(-x)=log4(4x+1)-(k-1)x,
令x=1,即log4$\frac{5}{4}$+(k-1)=log45-(k-1),
∴2(k-1)=1,
解得k=$\frac{3}{2}$;
∴f(x)=log4(4x+1)-$\frac{1}{2}$x,
根据函数f(x)是定义域上的偶函数,
∴当x=0时f(x)的值最小,最小值为f(0)=log42=$\frac{1}{2}$;
(2)∵g(x)=log4(a•2x-$\frac{4}{3}$a)(a≠0),
f(x)=log4(4x+1)-$\frac{1}{2}$x=log4(4x+1)-log4(2x)=log4$\frac{{4}^{x}+1}{{2}^{x}}$,
令f(x)=g(x),则
log4$\frac{{4}^{x}+1}{{2}^{x}}$=log4(a•2x-$\frac{4}{3}$a),
∴$\frac{{4}^{x}+1}{{2}^{x}}$=a•2x-$\frac{4}{3}$a,
不妨设t=2x,t>0;
∴$\frac{{t}^{2}+1}{t}$=at-$\frac{4}{3}$a,
即t2+1=at2-$\frac{4}{3}$at,
整理,得(a-1)t2-$\frac{4}{3}$at-1=0,
设u(t)=(a-1)t2-$\frac{4}{3}$at-1,t>0;
两函数图象有公共点,等价于函数u(t)有正实数根,
①当a=1时 t=-$\frac{3}{4}$不满足题意,舍去;
②当△=0时 a=$\frac{3}{4}$ 或a=-3,
若a=$\frac{3}{4}$,则t=-$\frac{1}{2}$<0不满足题意,舍去;
若a=-3,则t=$\frac{1}{2}$满足题意,
③当一正根一负根时,有根的分布情况得(a-1)•u(0)<0,
∴a>1,
综上,a=-3或a>1时,两函数的图象有1个交点;
④当有两个正根时,$\left\{\begin{array}{l}{{\frac{16}{9}a}^{2}+4(a-1)>0}\\{\frac{4a}{3(a-1)}>0}\\{\frac{-1}{a-1}>0}\end{array}\right.$,
解得a<-3,此时两函数图象有2个交点;
∴当函数f(x)与g(x)的图象有交点时,a的取值范围是{a|a≤-3或a>1};
(3)由(2)知,a=-3或a>1时,函数f(x)与g(x)的图象有1个交点,
a<-3时,函数f(x)与g(x)的图象有2个交点.
点评 本题考查了函数的奇偶性的应用问题,也考查了函数的图象与性质的应用问题,考查了方程思想与转化思想的应用问题,是综合性题目.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案(1)若要获利最大年利润,售价应定为多少万元/辆?
(2)该销售店为了提高销售业绩,推出了分期付款的促销活动.已知销售一辆该品牌的汽车,若一次性付款,其利润为2万元;若分2期或3期付款,其利润为2.5万元;若分4期或5期付款,其利润为3万元.该销售店对最近分期付款的10位购车情况进行了统计,统计结果如下表.
| 付款方式 | 一次性 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 1 | 1 | 3 | 2 | 3 |
 如图所示,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=$\frac{1}{2}$AE.设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[$\frac{π}{6}$,$\frac{π}{4}$],则当k取最大值时,平面BDE与平面ABC所成角的正切值为( )
如图所示,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=$\frac{1}{2}$AE.设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[$\frac{π}{6}$,$\frac{π}{4}$],则当k取最大值时,平面BDE与平面ABC所成角的正切值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
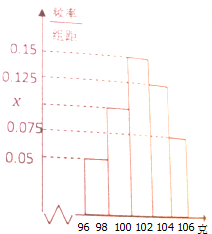 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).