题目内容
10.直线l过点P(2,1),按下列条件求直线l的方程(1)直线l与直线x-y+1=0垂直;
(2)直线l在两个坐标轴上的截距相等.
分析 (1)直线l与直线x-y+1=0垂直,可设直线l的方程为x+y+m=0,把点P(2,1)代入解得m即可得出.
(2)当直线l经过原点时,直线l的方程为:y=$\frac{1}{2}$x.当直线l不经过原点时,设直线l的方程为:x+y=a,把点P(2,1)代入解得a即可得出.
解答 解:(1)∵直线l与直线x-y+1=0垂直,
∴可设直线l的方程为x+y+m=0,
把点P(2,1)代入:2+1+m=0,解得m=-3.
∴直线l的方程为x+y-3=0.
(2)当直线l经过原点时,直线l的方程为:y=$\frac{1}{2}$x,即x-2y=0.
当直线l不经过原点时,设直线l的方程为:x+y=a,
把点P(2,1)代入:2+1=a,解得a=3.
∴直线l的方程为x+y-3=0.
综上可得:直线l的方程为x+y-3=0或x-2y=0.
点评 本题考查了直线的斜率、截距式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
20.i为虚数单位,复数$\frac{i}{i+1}$在复平面内对应的点到原点的距离为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
19.设{an}是等比数列,且a3=$\frac{3}{2}$,S3=$\frac{9}{2}$,则q=( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | 1或-$\frac{1}{2}$ | D. | 1或$\frac{1}{2}$ |
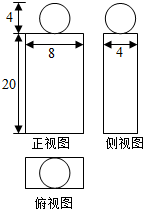 己知一几何体的三视图,试根据三视图计算出它的表面积和体积(结果保留π).
己知一几何体的三视图,试根据三视图计算出它的表面积和体积(结果保留π).