题目内容
18.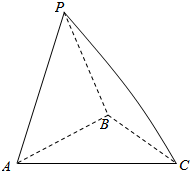 如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.
如图所示的三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$.(1)求其体积.(一直线和一平面内两相交直线垂直,则直线与平面垂直)
(2)求点P到面ABC的距离.
分析 (1)三棱锥P-ABC的三条侧棱两两垂直,利用三棱锥的体积公式,即可求其体积;
(2)利用等体积求点P到面ABC的距离.
解答 解:(1)∵三棱锥P-ABC的三条侧棱两两垂直,且PB=1,PA=$\sqrt{3}$,PC=$\sqrt{6}$,
∴VP-ABC=$\frac{1}{3}•\frac{1}{2}•1•\sqrt{3}•\sqrt{6}$=$\frac{\sqrt{2}}{2}$;
(2)△ABC的三边长为2,3,$\sqrt{7}$,∴cosB=$\frac{4+9-7}{2×2×3}$=$\frac{1}{2}$,
∴sinB=$\frac{\sqrt{3}}{2}$,
∴S△ABC=$\frac{1}{2}×2×3×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
设点P到面ABC的距离是h,则$\frac{1}{3}•\frac{3\sqrt{3}}{2}h=\frac{\sqrt{2}}{2}$,∴h$\frac{\sqrt{6}}{3}$.
点评 本题考查三棱锥体积的计算,考查点到平面的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.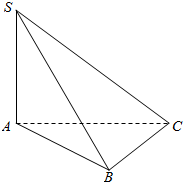 如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
 如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )
如图所示,在三棱锥S-ABC中,△ABC是等腰三角形,AB=BC=2a,∠ABC=120°,SA=2a,且SA⊥平面ABC,则点A到平面SBC的距离为( )| A. | $\frac{3a}{2}$ | B. | $\frac{2\sqrt{21}}{7}$a | C. | $\frac{5a}{2}$ | D. | $\frac{7a}{2}$ |
6.下列说法错误的是( )
| A. | 若棱柱的底面边长相等,则它的各个侧面的面积相等 | |
| B. | 九棱柱有9条侧棱,9个侧面,侧面为平行四边形 | |
| C. | 六角螺帽、三棱镜的外形都是棱柱 | |
| D. | 正四棱台的侧面不一定是等腰梯形 |
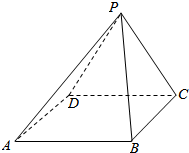 在正四棱锥P-ABCD中,AB=2.
在正四棱锥P-ABCD中,AB=2. 已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$. 在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC
在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC